题目内容
【题目】如图，在方格纸中，A，B，C三点都在小方格的顶点上（每个小方格的边长为1）． 
（1）在图甲中画一个以A，B，C为其中三个顶点的平行四边形，并求出它的周长． 
（2）在图乙中画一个经过A，B，C三点的圆，并求出圆的面积． 
【答案】
（1）解：如图甲，ABCD即为所求作平行四边形，
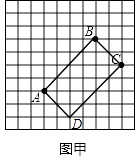
其周长为2（AD+CD）=2（2 
+4 ）=12
（2）解：如图乙，
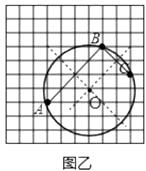
⊙O即为所求作圆，
其面积为π（ 
）2=10π
【解析】（1）根据平行四边形的定义即可求得，由周长公式计算即可得；（2）先确定圆心，再确定半径即可得圆，最后根据圆的面积公式可得答案．
【考点精析】利用勾股定理的概念和平行四边形的性质对题目进行判断即可得到答案，需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分．
练习册系列答案
相关题目
