��Ŀ����
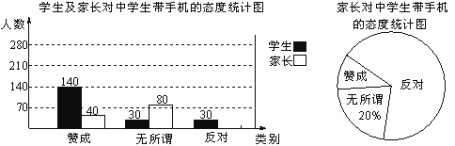
����Ŀ��ij��ʵʩ��ҵ����ƶ������ƶ�����а���ɽ��ֲijƷ�����֣���֪�����ֵijɱ���Ϊ6Ԫ/ǧ�ˣ������ջ�Ͷ���г�����ʱ�������г�������ָ����ֲ����������ÿ���������y��ǧ�ˣ������۵���x��Ԫ��֮��ĺ�����ϵ��ͼ��ʾ��
��1����y��x�ĺ�����ϵʽ����д��x��ȡֵ��Χ��
��2������Ʒ�����ֶ���Ϊ����ʱ��ÿ�����ۻ�õ����������������Ƕ��٣�
��3��ij��ũ�����깲��ժ����12000ǧ�ˣ�����Ʒ�����ֵı�����Ϊ50�죬���գ�2�������۷�ʽ���ܷ��ڱ�������ȫ���������������֣����ܣ���˵�����ɣ������ܣ�Ӧ�����ۼ�Ϊ����Ԫʱ���������������ܻ���������

���𰸡���1��y����20x+500����x��6������2����x��15.5ʱ��w�����ֵΪ1805Ԫ����3����x��13ʱ��w��1680����ʱ���������������ܻ���������
��������
��1�����㣨15��200������10��300������һ�κ�������ʽ��y��kx+b������⣻
��2��������ã�w��y��x��6������20��x��25����x��6�����ߩ�20��0����w�����ֵ��������⣻
��3����x��15.5ʱ��y��190��50��190��12000���ʣ����գ�2�������۷�ʽ�������ڱ�������ȫ�������ꣻ��50��500��20x����12000����ã�x��13����x��13ʱ���������������ܻ���������
�⣺��1�����㣨15��200������10��300������һ�κ�������ʽ��y��kx+b�ã�![]() ��
��
��ã�![]() ��
��
���������ı���ʽΪ��y����20x+500����x��6����
��2���裺��Ʒ�����ֶ���ΪxԪʱ��ÿ�����ۻ�õ�����w���
��w��y��x��6������20��x��25����x��6����
�ߩ�20��0����w�����ֵ��
��x����![]() ��
��![]() ��15.5ʱ��w�����ֵΪ1805Ԫ��
��15.5ʱ��w�����ֵΪ1805Ԫ��
��3����x��15.5ʱ��y��190��
50��190��12000��
�ʣ����գ�2�������۷�ʽ�������ڱ�������ȫ�������ꣻ
�裺Ӧ�����ۼ�ΪxԪʱ���������������ܻ���������w��
������ã�50��500��20x����12000����ã�x��13��
w����20��x��25����x��6����
��x��13ʱ��w��1680��
��ʱ���������������ܻ���������

 �������Ӧ���⼯ѵϵ�д�
�������Ӧ���⼯ѵϵ�д� �ۺ��Բ�ϵ�д�
�ۺ��Բ�ϵ�д�����Ŀ����ˮ������������ijˮ���깺��һ����ˮ��������Ϊ20Ԫ/ǧ�ˣ��ۼ۲�����20Ԫ/ǧ�ˣ��Ҳ�����32Ԫ/ǧ�ˣ�����������������ָ�ˮ��һ���������y��ǧ�ˣ��������ۼ�x��Ԫ/ǧ�ˣ��������±���ʾ��һ�κ�����ϵ��
������y��ǧ�ˣ� | �� | 34.8 | 32 | 29.6 | 28 | �� |
�ۼ�x��Ԫ/ǧ�ˣ� | �� | 22.6 | 24 | 25.2 | 26 | �� |
��1��ij������ˮ�����ۼ�Ϊ23.5Ԫ/ǧ�ˣ������ˮ������������
��2�����ij����������ˮ������150Ԫ����ô����ˮ�����ۼ�Ϊ����Ԫ��