��Ŀ����
����Ŀ��ijУ�Ƽ�ʵ����������ʵ���豸��С���IJ�����������
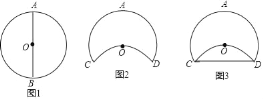
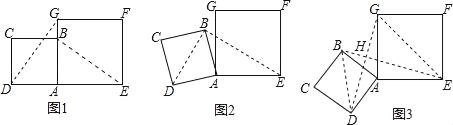
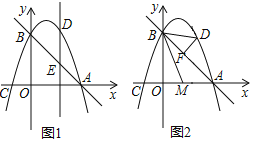
��С��ȡ����ʦ�ṩ��Բ��ϸ���������ҵ�Բ��O���������ҳ�ԲO��һ��ֱ�����ΪAB����ͼ1����������AB��8���ף�
�ڽ�Բ�����з���ʹ��B����Բ��O��λ�ã����۲��ֵ�Բ����δ���۵�Բ����������ֱ���ΪC��D����ͼ2����
����һϸ������C��D���㣨��ͼ3����
�ܼ������CD�ij��ȣ�
С��������CD�ij���Ϊ��������
A. 4![]() ����B. 2
����B. 2![]() ����C. 2
����C. 2![]() ����D. 3
����D. 3![]() ����
����
���𰸡�A
��������
��OE��CD��E����O��F��֤����OCF�ǵȱ������μ��ɽ�����⣮
�⣺��OE��CD��E����O��F��
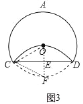
��CD��ֱƽ��OF��
��CO��CF��
��CO��CF��OF��
���OCF�ǵȱ������Σ�
��OC��4��
��CE��OCcos30����2![]() ��
��
��OE��CD��
��CE��ED��
��CD��2CE��4![]() ��
��
��ѡ��A��

��ϰ��ϵ�д�
 ����ͬ�����Ծ�ϵ�д�
����ͬ�����Ծ�ϵ�д�
�����Ŀ
����Ŀ���±���¼��һ����Ա�ڷ�������Ͷ���Ľ������ô��ԱͶ��һ�Σ�Ͷ�еĸ���Լ��( )
Ͷ������ | 10 | 50 | 100 | 150 | 200 | 250 | 300 | 500 |
Ͷ�д��� | 4 | 35 | 60 | 78 | 104 | 123 | 152 | 251 |
Ͷ��Ƶ�� | 0.40 | 0.70 | 0.60 | 0.52 | 0.52 | 0.49 | 0.51 | 0.50 |
A. 0.7B. 0.6C. 0.5D. 0.4