题目内容
【题目】在平面直角坐标系xOy中,函数y=![]() (x>0)的图象G经过点A(4,1),直线l:y=
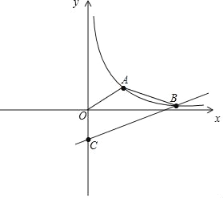
(x>0)的图象G经过点A(4,1),直线l:y=![]() x+b与图象G交于点B,与y轴交于点C.我们把横、纵坐标都是整数的点叫做整数点,记图象G在点A,B之间的部分与线段OA,OC,BC围成的区域(不含边界)为W,若b=﹣2,则区域W内的整数点的个数为_____;
x+b与图象G交于点B,与y轴交于点C.我们把横、纵坐标都是整数的点叫做整数点,记图象G在点A,B之间的部分与线段OA,OC,BC围成的区域(不含边界)为W,若b=﹣2,则区域W内的整数点的个数为_____;
【答案】10
【解析】
根据题意可以求得k的值和画出一次函数和反比例函数的图象,然后求出点C和点B的坐标,即可写出区域W内的整数点的坐标,本题得以解决.
解:∵点A(4,1)在函数y=![]() (x>0)的图象G上,
(x>0)的图象G上,
∴1=![]() ,得k=4,
,得k=4,
∴y=![]() ,
,
∵b=﹣2,
∴y=![]() x﹣2,
x﹣2,
当x=0时,y=﹣2,当y=0时,x=8,
∴点C(0,﹣2),y=![]() x﹣2与x轴的交点坐标为(8,0),
x﹣2与x轴的交点坐标为(8,0),
由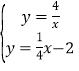 ,得
,得![]() 或
或![]() (舍去),
(舍去),
∴点B的坐标为(4+4![]() ,
,![]() ﹣1),
﹣1),
令![]() x﹣2=﹣1,得x=4,
x﹣2=﹣1,得x=4,
∴区域W内的整数点的坐标为(1,0),(1,﹣1),(2,0),(2,﹣1),(3,0),(3,﹣1),(4,0),(5,0),(6,0),(7,0),
∴区域W内的整数点的个数是10,
故答案为:10.

 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案【题目】在水果销售旺季,某水果店购进一优质水果,进价为20元/千克,售价不低于20元/千克,且不超过32元/千克,根据销售情况,发现该水果一天的销售量y(千克)与该天的售价x(元/千克)满足如下表所示的一次函数关系.
销售量y(千克) | … | 34.8 | 32 | 29.6 | 28 | … |
售价x(元/千克) | … | 22.6 | 24 | 25.2 | 26 | … |
(1)某天这种水果的售价为23.5元/千克,求当天该水果的销售量.
(2)如果某天销售这种水果获利150元,那么该天水果的售价为多少元?
【题目】已知二次函数y=ax2+bx﹣3的图象经过点(﹣1,0),(3,0).
(1)求此二次函数的解析式;
(2)在直角坐标系中描点,并画出该函数图象;
x | … | _____ | ____ | ____ | _____ | _____ | … |
y | … | _____ | ____ | ____ | ____ | _____ | … |
(3)根据图象回答:当函数值y<0时,求x的取值范围.