Question

【题目】已知抛物线的对称轴是直线x＝﹣1，与x轴一个交点是点A（﹣3，0），且经过点B（﹣2，6）

（1）求该抛物线的解析式；

（2）若点（﹣，y1）与点（2，y2）都在该抛物线上，直接写出y1与y2的大小关系．

Answer 1

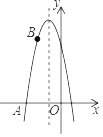
【答案】（1）y＝﹣2x2﹣4x+6；（2）y1＞y2．

【解析】

（1）先利用对称性确定抛物线与x轴另一个交点坐标为（1，0），则可设交点式为y＝a（x+3）（x﹣1），然后把B点坐标代入求出a即可；

（2）根据二次函数的性质，通过比较点（﹣，y1）和点（2，y2）到直线x＝﹣1的距离大小确定y1与y2的大小关系．

解：（1）∵抛物线的对称轴是直线x＝﹣1，与x轴一个交点是点A（﹣3，0），

∴抛物线与x轴另一个交点坐标为（1，0），

设抛物线解析式为y＝a（x+3）（x﹣1），

把B（﹣2，6）代入得a×1×（﹣3）＝6，解得a＝﹣2，

∴抛物线解析式为y＝﹣2（x+3）（x﹣1），即y＝﹣2x2﹣4x+6；

（2）∵点（﹣，y1）到直线x＝﹣1的距离比点（2，y2）到直线x＝﹣1的距离要小，

而抛物线的开口向下，

∴y1＞y2．