题目内容
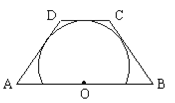
【题目】如图，
点在梯形
的下底
上，且与梯形的上底及两腰都相切，若
，则梯形的周长等于 。
【答案】
【解析】
由题意得DF=DE= HO =1，设半径为r，在Rt△AOE和Rt△DAH中，分别用勾股定理得到关于r和AE的式子，联立可消去r，解出AE的长，又由BG=AE，可求得梯形周长.
解：
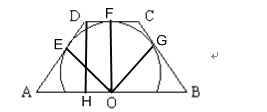
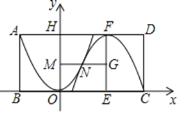
如图所示：点E、F、G分别为切点，链接OE、OF、OG，过D作DH⊥AB于H，
根据题意可知梯形
为等腰梯形，
，则DF=DE= HO =1，OA=2.5
OF⊥CD，OE⊥AD，设圆的半径为r，
在Rt△AOE中，由勾股定理得：
，
在Rt△DAH中，由勾股定理得：
，
整理可得：
，解得AE=1.5cm（负值已舍去），
∴BG=AE=1.5cm，梯形的周长=AB+BG+GC+CD+DE+EA=12cm.
练习册系列答案
相关题目
【题目】下表记录了一名球员在罚球线上投篮的结果，这么球员投篮一次，投中的概率约是( )
投篮次数 | 10 | 50 | 100 | 150 | 200 | 250 | 300 | 500 |
投中次数 | 4 | 35 | 60 | 78 | 104 | 123 | 152 | 251 |
投中频率 | 0.40 | 0.70 | 0.60 | 0.52 | 0.52 | 0.49 | 0.51 | 0.50 |
A. 0.7B. 0.6C. 0.5D. 0.4
