Question

【题目】在平面直角坐标系xOy中的点P和图形M，给出如下的定义：若在图形M上存在一点Q，使得P、Q两点间的距离小于或等于1，则称P为图形M的关联点．
（1）当⊙O的半径为2时，
①在点P1（ ，0），P2（ ， ），P3（ ，0）中，⊙O的关联点是 ．
②点P在直线y=﹣x上，若P为⊙O的关联点，求点P的横坐标的取值范围．
（2）⊙C的圆心在x轴上，半径为2，直线y=﹣x+1与x轴、y轴交于点A、B．若线段AB上的所有点都是⊙C的关联点，直接写出圆心C的横坐标的取值范围．

Answer 1

【答案】
（1）[ "解：①P2 ， P3
②根据定义分析，可得当最小y=﹣x上的点P到原点的距离在1到3之间时符合题意，
∴设P（x，﹣x），当OP=1时，
由距离公式得，OP= =1，
∴x= ，
当OP=3时，OP= =3，
解得：x=± ；
∴点P的横坐标的取值范围为：﹣ ≤≤﹣ ，或 ≤x≤ （2）

解：∵直线y=﹣x+1与x轴、y轴交于点A、B，

∴A（1，0），B（0，1），

如图1，

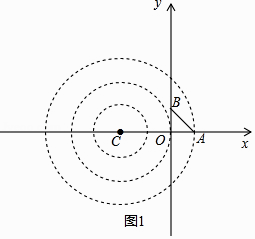
当圆过点A时，此时，CA=3，

∴C（﹣2，0），

如图2，

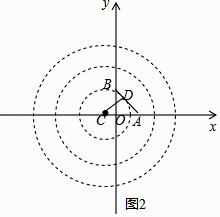
当直线AB与小圆相切时，切点为D，

∴CD=1，

∵直线AB的解析式为y=﹣x+1，

∴直线AB与x轴的夹角=45°，

∴AC= ，

∴C（1﹣ ，0），

∴圆心C的横坐标的取值范围为：﹣2≤xC≤1﹣ ；

如图3，

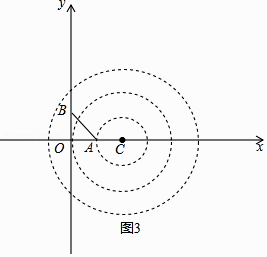
当圆过点A，则AC=1，∴C（2，0），

如图4，

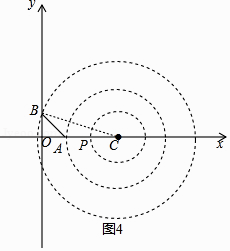
当圆过点B，连接BC，此时，BC=3，

∴OC= =2 ，

∴C（2 ，0）．

∴圆心C的横坐标的取值范围为：2≤xC≤2 ；

综上所述；圆心C的横坐标的取值范围为：﹣2≤xC≤1﹣ 或2≤xC≤2

【解析】（1）①∵点P1（ ，0），P2（ ， ），P3（ ，0），
∴OP1= ，OP2=1，OP3= ，
∴P1与⊙O的最小距离为 ，P2与⊙O的最小距离为1，OP3与⊙O的最小距离为 ，
∴⊙O，⊙O的关联点是P2 ， P3；
所以答案是：P2 ， P3；
【考点精析】通过灵活运用一次函数的图象和性质和勾股定理的概念，掌握一次函数是直线，图像经过仨象限；正比例函数更简单,经过原点一直线；两个系数k与b,作用之大莫小看，k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减；k为负来左下展,变化规律正相反；k的绝对值越大,线离横轴就越远；直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2即可以解答此题．