题目内容
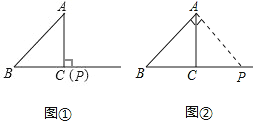
【题目】已知:如图,在Rt△ABC中,∠C=90°,AB=5cm,AC=3cm,动点P从点B出发沿射线BC以1cm/s的速度移动,设运动的时间为t秒.

(1)求BC边的长;
(2)当△ABP为直角三角形时,求t的值;
(3)当△ABP为等腰三角形时,求t的值
【答案】
【解析】试题分析:(1)直接根据勾股定理求出BC的长度;
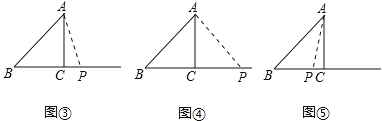
(2)当△ABP为直角三角形时,分两种情况:①当∠APB为直角时,②当∠BAP为直角时,分别求出此时的t值即可;
(3)当△ABP为等腰三角形时,分三种情况:①当AB=BP时;②当AB=AP时;③当BP=AP时,分别求出BP的长度,继而可求得t值.
试题解析:(1)在Rt△ABC中,BC2=AB2-AC2=52-32=16,
∴BC=4(cm);
(2)由题意知BP=tcm,
①当∠APB为直角时,点P与点C重合,BP=BC=4cm,即t=4;
②当∠BAP为直角时,BP=tcm,CP=(t-4)cm,AC=3cm,
在Rt△ACP中,
AP2=32+(t-4)2,
在Rt△BAP中,AB2+AP2=BP2,
即:52+[32+(t-4)2]=t2,
解得:t=![]() ,
,
故当△ABP为直角三角形时,t=4或t=![]() ;
;
(3)①当AB=BP时,t=5;
②当AB=AP时,BP=2BC=8cm,t=8;
③当BP=AP时,AP=BP=tcm,CP=|t-4|cm,AC=3cm,
在Rt△ACP中,AP2=AC2+CP2,
所以t2=32+(t-4)2,
解得:t=![]() ,
,
综上所述:当△ABP为等腰三角形时,t=5或t=8或t=![]() .
.

【题目】某公司计划从甲、乙两种产品中选择一种生产并销售,每年产销 x 件,已知产销两种产品的有关信息 如下:
产品 | 每件售价/万元 | 每件成本/万元 | 年最大产销量/件 |
甲 | 6 | 3 | 200 |
乙 | 20 | 10 | 80 |
甲、乙两产品每年的其他费用与产销量的关系分别是: y1 kx b 和 y2 ax2 m ,它们的函数图象分别如图(1)和图(2)所示.


(1)求: y1 、 y2 的函数解析式;
(2)分别求出产销两种产品的最大利润;(利润=销售额-成本-其它费用)
(3)若通过技术改进,甲产品的每件成本降到 a 万元,乙产品的年最大产销量可以达到 110 件,其它都不变,为获得最大利润,该公式应该选择产销哪种产品?请说明理由.