题目内容
【题目】如图,点A的坐标为(﹣8,0),点P的坐标为 ![]() ,直线y=
,直线y= ![]() x+b过点A,交y轴于点B,以点P为圆心,以PA为半径的圆交x轴于点C.
x+b过点A,交y轴于点B,以点P为圆心,以PA为半径的圆交x轴于点C.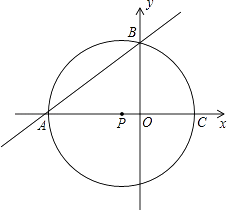
(1)判断点B是否在⊙P上?说明理由.
(2)求过A、B、C三点的抛物线的解析式;并求抛物线与⊙P另外一个交点为D的坐标.
(3)⊙P上是否存在一点Q,使以A、P、B、Q为顶点的四边形是菱形?若存在,求出点Q的坐标;若不存在,请说明理由.
【答案】
(1)
解:∵A(﹣8,0)在直线y= ![]() x+b上,则有b=6,
x+b上,则有b=6,
∴点B(0,6),即OB=6,
在Rt△BOP中,由勾股定理得PB= ![]() ,则PB=PA,
,则PB=PA,
∴点B在⊙P上
(2)
解:AC=2PA= ![]() ,则OC=
,则OC= ![]() ,点C
,点C ![]() ,
,
抛物线过点A、C,则设所求抛物线为y=a(x+8)(x﹣ ![]() ),代入点C
),代入点C ![]() ,则有a=
,则有a= ![]() ,
,
抛物线的解析式为y=﹣ ![]() x2﹣
x2﹣ ![]() x+6,
x+6,
直线x= ![]() 是抛物线和圆P的对称轴,点B的对称点为D,由对称可得D
是抛物线和圆P的对称轴,点B的对称点为D,由对称可得D ![]()
(3)
解:当点Q在⊙P上时,有PQ=PA= ![]() ,
,
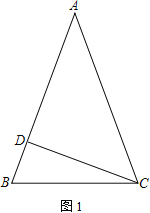
如图1所示,假设AB为菱形的对角线,那么PQ⊥AB且互相平分,由勾股定理得PE= ![]() ,则2PE≠PQ,所以四边形APBQ不是菱形.
,则2PE≠PQ,所以四边形APBQ不是菱形.
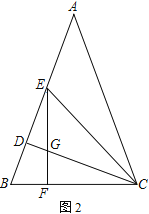
如图2所示,假设AB、AP为菱形的邻边,则AB≠AP,所以四边形APQB不是菱形.
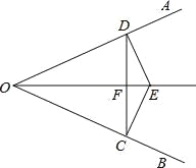
如图3所示,假设 AB、BP为菱形的邻边,则AB≠BP,所以四边形AQPB不是菱形.
综上所述,⊙P上不存在点Q,使以A、P、B、Q为顶点的四边形.
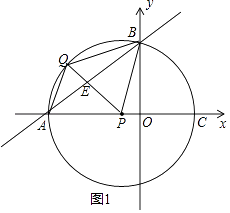
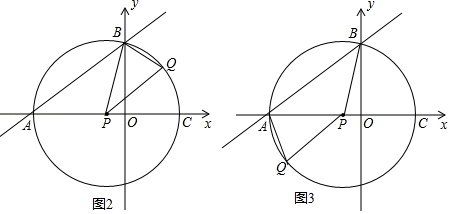
【解析】(1)把A(﹣8,0)代入y= ![]() x+b得到点B(0,6),即OB=6,根据勾股定理即可得到结论;(2)AC=2PA=
x+b得到点B(0,6),即OB=6,根据勾股定理即可得到结论;(2)AC=2PA= ![]() ,则OC=
,则OC= ![]() ,点C
,点C ![]() ,得到抛物线的解析式为y=﹣
,得到抛物线的解析式为y=﹣ ![]() x2﹣
x2﹣ ![]() x+6,直线x=
x+6,直线x= ![]() 是抛物线和圆P的对称轴,于是得到结论;(3)当点Q在⊙P上时,有PQ=PA=
是抛物线和圆P的对称轴,于是得到结论;(3)当点Q在⊙P上时,有PQ=PA= ![]() ,如图1所示,假设AB为菱形的对角线,如图2所示,假设AB、AP为菱形的邻边,如图3所示,假设 AB、BP为菱形的邻边,于是得到结论.
,如图1所示,假设AB为菱形的对角线,如图2所示,假设AB、AP为菱形的邻边,如图3所示,假设 AB、BP为菱形的邻边,于是得到结论.
【考点精析】掌握勾股定理的概念是解答本题的根本,需要知道直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.

 名校课堂系列答案
名校课堂系列答案【题目】2018年10月17日是我国第五个“扶贫日”,某校学生会干部对学生倡导的“扶贫”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,对学校部分捐款人数进行调查和分组统计后,将数据整理成如图所示的统计图,(图中信息不完整),已知A.B两组捐款人数的比为1:5.
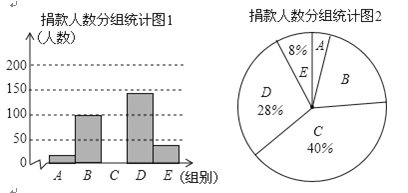
被调查的捐款人数分组统计表:
组别 | 捐款额x/元 | 人数 |
A | 1≤x<10 | a |
B | 10≤x<20 | 100 |
C | 20≤x<30 | ______ |
D | 30≤x<40 | ______ |
E | 40≤x | ______ |
请结合以上信息解答下列问题:
(1)求a的值和参与调查的总人数;
(2)补全“被调查的捐款人数分组统计图1”并计算扇形B的圆心角度数;
(3)已知该校有学生2200人,请估计捐款数不少于30元的学生人数有多少人?