题目内容
【题目】已知:如图,在四边形ABCD中,∠BAD=∠CDA,AB=DC= ![]() ,CE=a,AC=b,求证:
,CE=a,AC=b,求证: 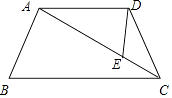
(1)△DEC∽△ADC;
(2)AEAB=BCDE.
【答案】
(1)证明:∵DC= ![]() ,CE=a,AC=b,
,CE=a,AC=b,
∴CD2=CE×CA,
即 ![]() =
= ![]() ,
,
又∵∠ECD=∠DCA,
∴△DEC∽△ADC;
(2)证明:∵△DEC∽△ADC,
∴∠DAE=∠CDE,
∵∠BAD=∠CDA,
∴∠BAC=∠EDA,
∵△DEC∽△ADC,
∴ ![]() =
= ![]() ,
,
∵DC=AB,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴△ADE∽△CAB,
∴ ![]() =
= ![]() ,
,
即AEAB=BCDE
【解析】(1)两组对应边的比相等且夹角对应相等的两个三角形相似,据此进行证明即可;(2)先根据相似三角形的性质,得出∠BAC=∠EDA, ![]() =
= ![]() ,再根据两组对应边的比相等且夹角对应相等的两个三角形相似,进行证明即可.
,再根据两组对应边的比相等且夹角对应相等的两个三角形相似,进行证明即可.
【考点精析】根据题目的已知条件,利用相似三角形的判定与性质的相关知识可以得到问题的答案,需要掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

 金博士一点全通系列答案
金博士一点全通系列答案【题目】某地区共有1800名初三学生,为了解这些学生的体质健康状况,开学之初随机选取部分学生进行体育测试,以下是根据测试成绩绘制的统计图表的一部分.
等级 | 测试成绩(分) | 人数 |
优秀 | 45≤x≤50 | 140 |
良好 | 37.5≤x<45 | 36 |
及格 | 30≤x<37.5 | |
不及格 | x<30 | 6 |

根据以上信息,解答下列问题:
(1)本次测试学生体质健康成绩为良好的有人,达到优秀的人数占本次测试总人数的百分比为%.
(2)本次测试的学生数为人,其中,体质健康成绩为及格的有人,不及格的人数占本次测试总人数的百分比为%.
(3)试估计该地区初三学生开学之初体质健康成绩达到良好及以上等级的学生数.
【题目】抛物线y=﹣x2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表所示:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,下列说法中,错误的是( )
A.抛物线于x轴的一个交点坐标为(﹣2,0)
B.抛物线与y轴的交点坐标为(0,6)
C.抛物线的对称轴是直线x=0
D.抛物线在对称轴左侧部分是上升的