题目内容
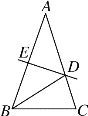
【题目】如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE,DF,EF.在此运动变化的过程中,有下列结论:
①△DFE是等腰直角三角形;
②四边形CEDF不可能为正方形;
③四边形CEDF的面积随点E位置的改变而发生变化;
④点C到线段EF的最大距离为 ![]() .
.
其中正确结论的个数是( )
A.1个
B.2个
C.3个
D.4个
【答案】B
【解析】连接CD,∵∠C=90°,AC=BC=4,∵△ABC是等腰直角三角形,∴∠A=∠B=45°,
∵D为AB的中点,∴CD⊥AB,CD=AD=BD,∴∠DCB=∠B=45°,∴∠A=∠DCF,
在△ADE和△CDF中,AE=CF,∠A=∠DCF,AD=CD ∴△ADE≌△CDF(SAS), ∴ED=DF,∠CDF=∠ADE,
∵∠ADE+∠EDC=90°, ∴∠EDC+∠CDF=90°,即∠EDF=90°, ∴△DFE是等腰直角三角形,所以①正确;
当E、F分别为AC、BC中点时,如图2,则AE=CE=CF=BF,DE=AE=CE, ∴CE=CF=DE=DF,
而∠ECF=90°, ∴四边形CDFE是正方形,所以②错误;
∵△ADE≌△CDF, ∴S△ADE=S△CDF,
∴S四边形CEDF=S△CDE+S△CDF=S△CDE+S△ADE=S△ADC= ![]() S△ABC=
S△ABC= ![]() ×
× ![]() ×4×4=4,所以③错误;
×4×4=4,所以③错误;
∵△CEF和△DEF都为直角三角形, ∴点C、D在以EF为直径的圆上,即点C、E、D、F四点在同一个圆上,
∵△DEF是等腰直角三角形,∴EF= ![]() DE,当DE⊥AC时,DE最短,此时DE=
DE,当DE⊥AC时,DE最短,此时DE= ![]() AC=2,
AC=2,
∴EF的最小值为2 ![]() ,即点C到EF的最小距离为
,即点C到EF的最小距离为 ![]() ,所以④正确.
,所以④正确.
连接CD,根据等腰直角三角形的性质得∠A=∠B=45°,根据等腰三角形的三线合一得CD⊥AB,CD=AD=BD,根据等边对等角得出∠DCB=∠B=45°,∴∠A=∠DCF,从而利用SAS判断出△ADE≌△CDF,根据全等三角形对应边,对应角相等得出ED=DF,∠CDF=∠ADE,根据等量代换得出∠EDF=90°,故△DFE是等腰直角三角形;当E、F分别为AC、BC中点时,如图2,则AE=CE=CF=BF,DE=AE=CE, 故CE=CF=DE=DF,
而∠ECF=90°, 从而知四边形CDFE是正方形;根据全等三角形的面积相等得出S△ADE=S△CDF,然后由S四边形CEDF=S△CDE+S△CDF=S△CDE+S△ADE=S△ADC= ![]() S△ABC;根据圆周角定理判断出点C、D在以EF为直径的圆上,即点C、E、D、F四点在同一个圆上,又△DEF是等腰直角三角形,根据勾股定理得出EF=
S△ABC;根据圆周角定理判断出点C、D在以EF为直径的圆上,即点C、E、D、F四点在同一个圆上,又△DEF是等腰直角三角形,根据勾股定理得出EF=![]() DE,当DE⊥AC时,DE最短,此时DE=
DE,当DE⊥AC时,DE最短,此时DE= ![]() AC=2,从而求出EF的最小值。
AC=2,从而求出EF的最小值。

 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案