题目内容
【题目】在半径为2cm的⊙O中，弦AB的长为2 
cm，则这条弦所对的圆周角为 ．
【答案】60°或120°
【解析】解：连接OA，过点O作OD⊥AB于点D，
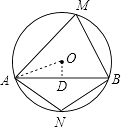
∵OA=2cm，AB=2 
cm，
∴AD=BD= ，
∴AD：OA= ：2，
∴∠AOD=60°，
∴∠AOB=120°，
∴∠AMB=60°，
∴∠ANB=120°．
所以答案是：60°或120°．
【考点精析】本题主要考查了垂径定理和圆周角定理的相关知识点，需要掌握垂径定理：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧；顶点在圆心上的角叫做圆心角;顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半才能正确解答此题．
练习册系列答案
科学实验活动册系列答案
相关题目
