题目内容
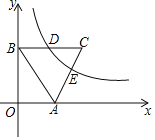
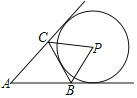
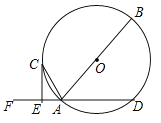
【题目】如图,![]() 是⊙
是⊙![]() 的直径,
的直径,![]() 是⊙
是⊙![]() 的弦,点
的弦,点![]() 是
是![]() 延长线的一点,
延长线的一点,![]() 平分
平分![]() 交⊙
交⊙![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,垂足为点
,垂足为点![]()
(1)求证:![]() 是⊙
是⊙![]() 的切线;
的切线;
(2)若![]() ,求⊙
,求⊙![]() 的半径.
的半径.
【答案】(1)见解析;(2)2.5
【解析】
(1)连接CO,易得∠OCA=∠OAC,由AC平分∠FAB,得∠CAE=∠OAC,从而得∠OCA=∠CAE,,进而即可得OC∥FD,即可得到结论;
(2)连接BC,由勾股定理得AC=![]() ,易得△ABC∽△ACE,从而得
,易得△ABC∽△ACE,从而得![]() ,进而即可求解.
,进而即可求解.
(1)连接CO,
∵OA=OC,
∴∠OCA=∠OAC,
∵AC平分∠FAB,
∴∠CAE=∠OAC,
∴∠OCA=∠CAE,
∴OC∥FD,
∵CE⊥DF,
∴OC⊥CE,
∴CE是⊙O的切线;
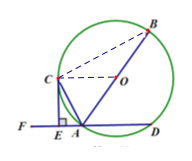
(2)连接BC,
在Rt△ACE中,AC=![]() ,
,
∵AB是⊙O的直径,
∴∠BCA=90°,
∴∠BCA=∠CEA,
∵∠CAE=∠CAB,
∴△ABC∽△ACE,
∴![]() ,
,
∴![]() ,
,
∴AB=5,
∴AO=2.5,即⊙O的半径为2.5.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
【题目】焦作市教育局为调查全市教师的运动情况,结合现今流行的“微信运动”,随机调查了本市![]() 名老师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表:
名老师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表:
步数 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
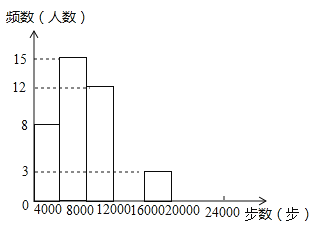
请根据以上信息,解答下列问题:
(1)写出![]() 的值,并补全频数分布直方图;
的值,并补全频数分布直方图;
(2)本市约有![]() 名教师,结合调查的数据估计日行走步数超过
名教师,结合调查的数据估计日行走步数超过![]() 步(包含
步(包含![]() 步)的教师有多少名?
步)的教师有多少名?
(3)若在被调查的教师中,选取日行走步数超过![]() 步(包含
步(包含![]() 步)的两名教师与大家分享心得,求被选取的两名教师恰好都在
步)的两名教师与大家分享心得,求被选取的两名教师恰好都在![]() 步(包含
步(包含![]() 步)以上的概率.
步)以上的概率.