题目内容
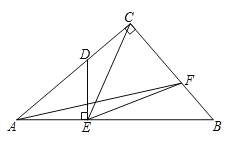
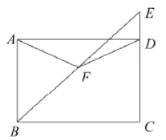
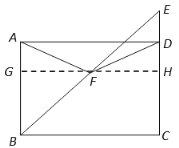
【题目】如图,在矩形![]() 中,延长
中,延长![]() 至点
至点![]() ,且
,且![]() ,
,![]() 为
为![]() 中点,连结
中点,连结![]() ,
,![]() .
.
(1)求证:![]() 的面积是
的面积是![]() 的面积的
的面积的![]() 倍.
倍.
(2)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)过点F作GH⊥CD,分别交AB,CD于点G,H.根据四边形ABCD是矩形,![]() 为
为![]() 中点,可证得△BGF≌△EHF,得GF=HF,△ABF的面积=
中点,可证得△BGF≌△EHF,得GF=HF,△ABF的面积=![]() ,△DEF的面积=
,△DEF的面积=![]() ,又因为AB=3DE,即可求证△ABF的面积是△DEF的面积的3倍.
,又因为AB=3DE,即可求证△ABF的面积是△DEF的面积的3倍.
(2)设DE=a,则CD=3a,BE=6a,EC=4a,由勾股定理即可求出a,进而求出BE.
(1)证明:过点F作GH⊥CD,分别交AB,CD于点G,H.
∵AB∥CD,∴∠GBF=∠E,∠BGF=∠EHF.
∵F为BE中点,∴BF=EF.
∴△BGF≌△EHF(AAS). ∴GF=HF.
∵FH⊥CD,AB∥CD,∴GF⊥AB.
∴△ABF的面积=![]() ,△DEF的面积=
,△DEF的面积=![]() ,
,
∵AB=3DE,GF=HF,
∴△ABF的面积是△DEF的面积的3倍.
(2)设DE=a,则CD=AB=3a,BE=2AB=6a,
∴EC=ED+CD=a+3a=4a.
由勾股定理,得![]() ,
,
即![]() ,解得
,解得![]() ,或
,或![]() (舍去).
(舍去).
∴![]() .
.
故答案为:![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】将正偶数按下表排成5列:
第一列 | 第二列 | 第三列 | 第四列 | 第五列 | |
第一行 | 2 | 4 | 6 | 8 | |
第二行 | 16 | 14 | 12 | 10 | |
第三行 | 18 | 20 | 22 | 24 | |
第四行 | 32 | 30 | 28 | 26 | |
…… |
根据上面规律,2020应在( )
A.125行,3列B.125行,2列C.253行,2列D.253行,3列