Question

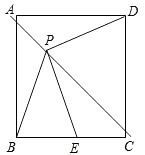
【题目】如图，正方形ABCD的边长为1cm，AC是对角线，AE平分∠BAC，EF⊥AC于F．
（1）求证：BE=EF．
（2）求tan∠EAF的值．

Answer 1

【答案】
（1）证明：∵在正方形ABCD中，EF⊥AC，AB⊥BC，

∴∠AFE=∠ABE=90°；

∵AE平分∠BAC，

∴∠BAE=∠FAE；　

又∵AE=AE，

∴Rt△BAE≌Rt△FAE，

故AB=AF，BE=FE

（2）解：∵正方形ABCD，

∴在Rt△CEF中，∠ECF=45°，

故FE=CF，

∴BE=CF，

∵正方形ABCD的边长为1 cm，对角线AC= cm，

由（1）可得，BE=EF=CF=AC﹣AF=AC﹣AB= ﹣1（cm），

∴

【解析】（1）根据角平分线上的点到角两边的距离相等，可得BE=EF；（2）根据勾股定理，计算正方形的对角线的长，减去AF的长求得CF的长，最后计算tan∠EAF的值．
【考点精析】解答此题的关键在于理解角平分线的性质定理的相关知识，掌握定理1：在角的平分线上的点到这个角的两边的距离相等； 定理2：一个角的两边的距离相等的点，在这个角的平分线上，以及对正方形的性质的理解，了解正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形．