题目内容
【题目】如图，抛物线y=﹣ 
x2+ 
x+2与x轴交于点A，B，与y轴交于点C．点P是线段BC上的动点（点P不与B，C重合），连接并延长AP交抛物线于另一点Q，设点Q的横坐标为x．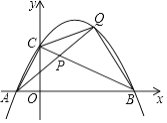
（1）①写出点A，B，C的坐标：A（），B（），C（）；
②求证：△ABC是直角三角形；
（2）记△BCQ的面积为S，求S关于x的函数表达式；
（3）在点P的运动过程中， 
是否存在最大值？若存在，求出 的最大值及点Q的坐标；若不存在，请说明理由．
【答案】
（1）﹣1，0；4，0；0，2
（2）
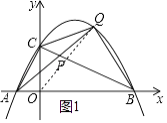
解：连接OQ，如图1所示．
设点Q的坐标为（x，﹣ 
x2+ 
x+2），
∴S=S△OCQ+S△OBQ﹣S△OBC= ×2x+ ×4（﹣ x2+ x+2）﹣ ×2×4=﹣x2+4x．
（3）
解：过点Q作QH⊥BC于H，如图2所示．
∵∠ACP=∠QHP=90°，∠APC=∠QPH，
∴△APC∽△QPH，
∴ 
= 
．
∵S△BCQ= BCQH= 
OH，
∴QH= 
，
∴ 
= 
= 
（﹣x2+4x）=﹣ （x﹣2）2+ 
，
∴当x=2时， 取最大值，最大值为 ，此时点Q的坐标为（2，3）．
【解析】解：（1）①当x=0时，y=﹣ x2+ x+2=2，
∴点C（0，2）．
当y=﹣ x2+ img src="https://thumb.zyjl.cn/questionBank/Upload/2017/08/15/11/610d3a99/SYS201708151152513446683969_DA/SYS201708151152513446683969_DA.003.png" width="9" height="32" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" /> x+2=0时，有x2﹣3x﹣4=（x+1）（x﹣4）=0，
解得：x1=﹣1，x2=4，
∴A（﹣1，0），B（4，0）．
所以答案是：﹣1，0；4，0；0，2．
②证明：∵A（﹣1，0），B（4，0），C（0，2），
∴AB=5，AC= ，BC=2 ，
∴AB2=25=AC2+BC2 ，
∴△ABC是直角三角形．
【题目】一辆汽车在公路上匀速行驶，下表记录的是汽车在加满油后油箱内余油量y（升）与行驶时间x（时）之间的关系：
行驶时间x（时） | 0 | 1 | 2 | 2.5 |
余油量y（升） | 100 | 80 | 60 | 50 |
（1）小明分析上表中所给的数据发现x，y成一次函数关系，试求出它们之间的函数表达式（不要求写出自变量的取值范围）；
（2）求汽车行驶4.2小时后，油箱内余油多少升？
