Question

【题目】如图，P是边长为1的正方形ABCD对角线AC上一动点（P与A、C不重合），点E在射线BC上，且PE=PB．设AP=x，△PBE的面积为y．则能够正确反映y与x之间的函数关系的图象是（ ）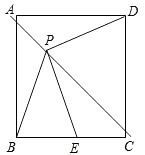

A.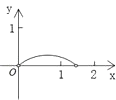
B.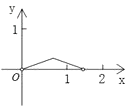
C.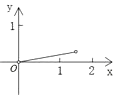
D.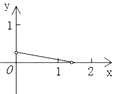

Answer 1

【答案】A
【解析】解：过点P作PF⊥BC于F，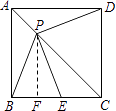

∵PE=PB，
∴BF=EF，
∵正方形ABCD的边长是1，
∴AC= = ，
∵AP=x，∴PC= ﹣x，
∴PF=FC= （ ﹣x）=1﹣ x，
∴BF=FE=1﹣FC= x，
∴S△PBE= BEPF= x（1﹣ x）=﹣ x2+ x，
即y=﹣ x2+ x（0＜x＜ ），
∴y是x的二次函数（0＜x＜ ），
故选A．
【考点精析】利用函数的图象对题目进行判断即可得到答案，需要熟知函数的图像是由直角坐标系中的一系列点组成；图像上每一点坐标（x，y）代表了函数的一对对应值，他的横坐标x表示自变量的某个值，纵坐标y表示与它对应的函数值．