��Ŀ����
����Ŀ������������֪��l��m��n��k��ƽ����l��m��m��n��n��k֮��ľ���ֱ�Ϊd1��d2��d3����d1��d3��1��d2��2.���ǰ��ĸ�����ֱ���l��m��n��k������ƽ�����ϵ��ı��γ�Ϊ�������ı��Ρ� ��
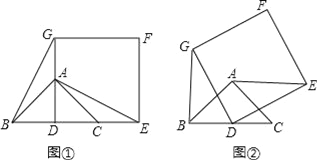
��̽��1��(1)��ͼ1��������ABCDΪ�������ı��Ρ���BE��l�ڵ�E��BE�ķ����ӳ��߽�ֱ��k�ڵ�F.��������ABCD�ı߳���
��̽��2��(2)��ͼ2������ABCDΪ�������ı��Ρ��ҡ�ADC��60�㣬��AEF�ǵȱ������Σ�AE��k�ڵ�E����AFD��90�㣬ֱ��DF�ֱ�ֱ��l��k�ڵ�G����M.��֤��EC��DF��
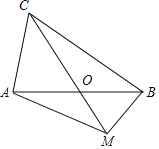
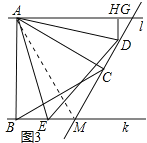
����չ��(3)��ͼ3��l��k���ȱߡ�ABC�Ķ���A��B�ֱ�����ֱ��l��k�ϣ�AB��k�ڵ�B���ҡ�ACD��90�㣬ֱ��CD�ֱ�ֱ��l��k�ڵ�G����M����D����E�ֱ����߶�GM��BM�ϵĶ��㣬��ʼ�ձ���AD��AE��DH��l�ڵ�H.���룺DH��ʲô��Χ�ڣ�BC��DE����˵����ʱBC��DE�����ɣ�

���𰸡���1��![]() ����2��֤������������3����2��DH��4ʱ��BC��DE�����ɼ�����.
����2��֤������������3����2��DH��4ʱ��BC��DE�����ɼ�����.
����������1��֤����ABE�ա�BCF���������AE�ij���Ȼ�����ù��ɶ���������⣻
��2����B��BE��l�ڵ�E����k�ڵ�F����֤��AEB�ס�BCF��Ȼ���AB�dz���AB�ǿ������������������ã�
��3������AC��֤��ֱ�ǡ�AEC��ֱ�ǡ�AFD����֤�ã�
��4������֤��AM��BC��Ȼ��֤��Rt��ABE��Rt��ACD���õ���BAE=��CAD����AM��ED������֤��BC��DE��
��1���⣺��l��k��BE��l��
���BFC=��BEA=90�㣬
���ABE+��BAE=90�㣬
���ı���ABCD�������Σ�
���ABC=90�㣬AB=BC��
���ABE+��CBF=90�㣬
���BAE=��CBF��
�ڡ�ABE�͡�BCF�У���BEA=��CFB����BAE=��CBF��AB=BC
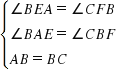
�����ABE�ա�BCF��AAS����
��AE=BF��
��d1=d3=1��d2=2��
��BE=3��AE=1��
��ֱ�ǡ�ABE�У�AB=![]() =
=![]() =
=![]() ��
��
�������εı߳���![]() ��
��
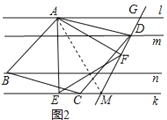
��2��֤��������AC����ͼ2��ʾ��
���ı���ABCD�����Σ��ҡ�ADC=60�㣬
��AC=AD��
�ߡ�AEF�ǵȱ������Σ�
��AE=AF��
��AE��k����AFD=90�㣬
���AEC=��AFD=90�㣬
��Rt��AEC��Rt��AFD��AC=AD��AE=AF��
![]() ��
��
��Rt��AEC��Rt��AFD��HL����
��EC=DF��
��3���⣺��2��DH��4ʱ��BC��DE���������£�
��ͼ3��ʾ����2��DH��4ʱ����D���߶�CM�ϣ�����AM��
���ABM=��ACM=90�㣬AB=AC��AM=AM��
��Rt��ABM��Rt��ACM��AM=AM��AB=AC��
![]() ��
��
��Rt��ABM��Rt��ACM��HL����
���BAM=��CAM��
��AM��BC��
��Rt��ABE��Rt��ACD��AE=AD��AB=AC��
![]() ��
��
��Rt��ABE��Rt��ACD��HL����
���BAE=��CAD��
���EAM=��DAM��
��AM��ED��
��BC��DE��
���㾦�����⿼����ȫ�������ε��ж��������Լ����������ε��ж������ʣ���ȷ�������Ƶ��������ǹؼ�������ʱ����������ȷ���������ߣ�

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�