题目内容
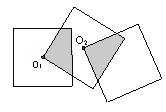
【题目】如图①,已知△ABC是等腰三角形,∠BAC=90°,点D是BC的中点,作正方形DEFG,使点A、C分别在DG和DE上,连接AE、BG.
(1)试猜想线段BG和AE的数量关系;
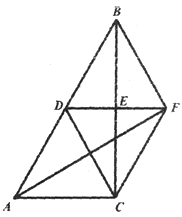
(2)如图②,将正方形DEFG绕点D按逆时针方向旋转α(0°<α≤90°),判断(1)中的结论是否仍然成立,证明你的结论.

(3)若BC=DE=2,在(2)的旋转过程中,求线段AE长的最大值和最小值
【答案】(1)证明见解析(2)成立(3)线段AE长的最大值是3,最小值是1.
【解析】整体分析:
(1)由等腰直角三角形的性质及正方形的性质就可以得出△ADE≌△BDG即可;(2)①如图2,连接AD,证明△ADE≌△BDG;(3)由(1)可知BG=AE,当BG取得最大值时,AE取得最大值,画出图形,根据图形求解.
解:(1)∵△ABC是等腰三角形,∴BD=DA,
∵四边形DEFG是正方形,所以GD=DE,∠GDB=∠EDA=90°;
∴△BDG≌△ADE;
∴BG=AE;
(2)成立,证明如下:
连接AD,
∵Rt△BAC中,D为斜边BC的中点,
∴AD=BD,AD⊥BC,∴∠ADG+∠GDB=90°,
∵EFGD为正方形,∴DE=DG,且∠GDE=90°,
∴∠ADG+∠ADE=90°,∴∠BDG=∠ADE,
△BDG和△AED中,BD=AD,∠BDG=∠ADE,GD=ED,
∴△BDG≌△ADE,
∴BG=AE;

(3)由(2)得BG=AE,当BG取得最大值时,AE取得最大值;
当旋转角度为270°时,如图,
BG的最大值为1+2=3,
所以AE的最大值为3;
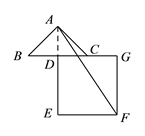
当旋转角度为90°时,如图,
BG的最小值为2-1=1,
所以AE的最小值为1.

所以线段AE长的最大值是3,最小值是1.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】阅读下列材料:
近五年,我国对外贸易发展迅速.据海关统计,2017年我国进出口总额为27.8万亿元,比2016年增长14.4%,其中2017年进口额12.5万亿元,比2016年增长19.0%.2013---2016年我国进出口额数据如下表:
年份 | 2013 | 2014 | 2015 | 2016 |
出口额/万亿元 | 13.7 | 14.4 | 14.1 | 13.8 |
进口额/万亿元 | 12.1 | 12.0 | 10.4 | 10.5 |
根据以上材料解答下列问题:
(1)2017年我国出口额为______________万亿元;
(2)请选择适当的统计图描述2013---2017年我国出口额,并在图中标明相应数据;
(3)通过(2)中的统计图判断:2013---2017年我国出口额比上一年增长最多的是_______________年.