题目内容
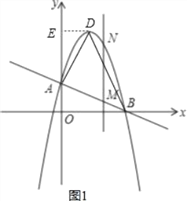
【题目】如图,直线AB分别交y轴、x轴于A、B两点,OA=2,tan∠ABO=![]() ,抛物线y=﹣x2+bx+c过A、B两点.
,抛物线y=﹣x2+bx+c过A、B两点.
(1)求直线AB和这个抛物线的解析式;
(2)设抛物线的顶点为D,求△ABD的面积;
(3)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N.求当t取何值时,MN的长度l有最大值?最大值是多少?

【答案】(1)y=﹣![]() x+2;(2)
x+2;(2)![]() (3)当t=2时,MN的长度l有最大值,最大值是4.
(3)当t=2时,MN的长度l有最大值,最大值是4.
【解析】(1)∵在Rt△AOB中,tan∠ABO=![]() ,OA=2,即
,OA=2,即![]() =
=![]() ,
,
∴0B=4,∴A(0,2),B(4,0),
把A、B的坐标代入y=﹣x2+bx+c得: ![]() ,解得:b=
,解得:b=![]() ,
,
∴抛物线的解析式为y=﹣x2+![]() x+2,
x+2,
设直线AB的解析式为y=kx+e,把A、B的坐标代入得: ![]() ,
,
解得:k=﹣![]() ,e=2,
,e=2,
所以直线AB的解析式是y=﹣![]() x+2;
x+2;
(2)过点D作DE⊥y轴于点E,
由(1)抛物线解析式为y=﹣x2+![]() x+2=﹣(x﹣
x+2=﹣(x﹣![]() )2+
)2+![]() ,
,
即D的坐标为(![]() ,
, ![]() ),则ED=
),则ED=![]() ,EO=
,EO=![]() ,AE=EO﹣OA=
,AE=EO﹣OA=![]() ,
,
S△ABD=S梯形DEOB﹣S△DEA﹣S△AOB=![]() ×(
×(![]() +4)×
+4)×![]() ﹣
﹣![]() ×
×![]() ×
×![]() ﹣
﹣![]() ×4×2=
×4×2=![]() ;
;
(3)由题可知,M、N横坐标均为t.
∵M在直线AB:y=﹣![]() x+2上,∴M(t,﹣
x+2上,∴M(t,﹣![]() t+2),
t+2),
∵N在抛物线y=﹣x2+![]() x+2上,∴M(t,﹣t2+
x+2上,∴M(t,﹣t2+![]() t+2),
t+2),
∵作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N,
∴MN=﹣t2+![]() t+2﹣(﹣
t+2﹣(﹣![]() +2)=﹣t2+4t=﹣(t﹣2)2+4,其中0<t<4,
+2)=﹣t2+4t=﹣(t﹣2)2+4,其中0<t<4,
∴当t=2时,MN最大=4,
所以当t=2时,MN的长度l有最大值,最大值是4.

【题目】为响应国家节能减排的号召,鼓励居民节约用电,各省市先后出台了居民用电“阶梯价格”制度,下表是某市的电价标准(每月).
阶梯 | 一户居民每月用电量x(单位:度) | 电费价格(单位:元/度) |
一档 | 0<x≤180 | a |
二档 | 180<x≤280 | b |
三档 | x>280 | 0.82 |
(1)已知小华家四月份用电200度,缴纳电费105元;五月份用电230度,缴纳电费122.1元,请你根据以上数据,求出表格中a,b的值;
(2)六月份是用电高峰期,小华家计划六月份电费支出不超过208元,那么小华家六月份最多可用电多少度?