Question

【题目】数形结合是解决数学问题的一种重要的思想方法，借助图的直观性，可以帮助理解数学问题．

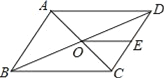
（1）请写出图1、图2、图3分别能解释的乘法公式．

（2）用4个全等的长和宽分别为、的长方形拼摆成一个如图4的正方形，请你写出这三个代数式、、之间的等量关系．

（3）根据（2）中你探索发现的结论，完成下列问题：

①当，时， 则 的值为 ．

②设，，计算：的结果．

Answer 1

【答案】（1）见解析；（2）－=4；（3）①±7，.

【解析】

（1）图1根据大正方形的面积等于被分成的四部分的面积的和进行解答；图2根据阴影面积=大正方形的面积-2个长方形的面积+小正方形的面积解答即可；图3根据两个图形中阴影部分的面积相等解答即可；

（2）根据大正方形的面积-阴影部分的面积=4个长方形的面积解答即可；

（3）①由（2）可知，=-4，代入计算即可；②由（2）可知， =4×A×B，代入计算即可；

解：(1) 图1：；图2：；

图3：;

（2）图4：－=4;

（3）①∵=-4=25+24=49，

∴a+b=±7；

②=4×A×B=4××=×

=.