题目内容
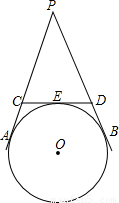如图，PA、PB、CD是⊙O的切线，A、B、E是切点，CD分别交线段PA、PB于C、D两点，若∠APB=40°，则∠COD的度数为（ ）A．50°
B．60°
C．70°
D．75°
【答案】分析：首先画出图形，连接OA、OC、OE、OD、OB，根据切线性质，∠P+∠AOB=180°，可知∠AOB=140°，再根据CD为切线可知∠COD=
∠AOB．
解答：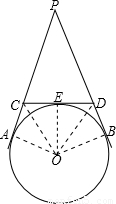
解：由题意得，连接OA、OC、OE、OD、OB，所得图形如下：
由切线性质得，OA⊥PA，OB⊥PB，OE⊥CD，DB=DE，AC=CE，
∵AO=OE=OB，
∴△AOC≌△EOC（SAS），△EOD≌△BOD（SAS），
∴∠AOC=∠EOC，∠EOD=∠BOD，
∴∠COD=
∠AOB，
∵∠APB=40°，
∴∠AOB=140°，
∴∠COD=70°．
故选C．
点评：本题考查了切线的性质，运用切线的性质来进行计算或论证，常通过作辅助线连接圆心和切点，利用垂直构造直角三角形解决有关问题，是基础题型．
∠AOB．解答：
解：由题意得，连接OA、OC、OE、OD、OB，所得图形如下：由切线性质得，OA⊥PA，OB⊥PB，OE⊥CD，DB=DE，AC=CE，
∵AO=OE=OB，
∴△AOC≌△EOC（SAS），△EOD≌△BOD（SAS），
∴∠AOC=∠EOC，∠EOD=∠BOD，
∴∠COD=
∠AOB，∵∠APB=40°，
∴∠AOB=140°，
∴∠COD=70°．
故选C．
点评：本题考查了切线的性质，运用切线的性质来进行计算或论证，常通过作辅助线连接圆心和切点，利用垂直构造直角三角形解决有关问题，是基础题型．
练习册系列答案
阅读快车系列答案
相关题目
如图，PA、PB是⊙O的切线，切点分别为A、B，点C在⊙O上，如果∠P=50°，那么∠ACB等于
6、如图，PA、PB分别切⊙O于点A、B，M是劣弧AB上的一个动点（点A、B除外），过M作⊙O的切线分别交PA、PB于点C、D．设CM的长为x，△PCD的周长为y，在下列图象中，大致表示y与x之间的函数关系的是（ ）
如图，PA、PB分别切⊙0于A、B，PA、BO的延长线交于点Q，连AB，若sin∠AQO=
如图，PA、PB是⊙O的切线，切点分别为A、B，若∠APB=40°，则∠ACB=