题目内容
 如图,PA、PB是⊙O的切线,切点分别为A、B,点C在⊙O上,如果∠P=50°,那么∠ACB等于
如图,PA、PB是⊙O的切线,切点分别为A、B,点C在⊙O上,如果∠P=50°,那么∠ACB等于分析:连接OA、OB.根据切线的性质,得到∠OAP=∠OBP=90°,根据四边形的内角和定理即可求得∠AOB,再进一步根据圆周角定理求解即可.
解答: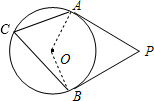 解:连接OA、OB;
解:连接OA、OB;
∵PA、PB是⊙O的切线,切点分别为A、B,
∴∠OAP=∠OBP=90°,
∴∠AOB=180°-∠P=130°,
∴∠ACB=
∠AOB=65°.
 解:连接OA、OB;
解:连接OA、OB;∵PA、PB是⊙O的切线,切点分别为A、B,
∴∠OAP=∠OBP=90°,
∴∠AOB=180°-∠P=130°,
∴∠ACB=
| 1 |
| 2 |
点评:此题主要是运用了切线的性质定理、四边形的内角和定理以及圆周角定理.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
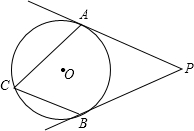 如图,PA,PB是⊙O的切线,切点分别为A,B,且∠APB=50°,点C是优弧
如图,PA,PB是⊙O的切线,切点分别为A,B,且∠APB=50°,点C是优弧
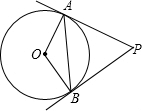 如图,PA、PB是⊙O的切线,A、B为切点,∠OAB=30度.
如图,PA、PB是⊙O的切线,A、B为切点,∠OAB=30度. 4、如图,PA、PB是⊙O的两条切线,A、B是切点,连接AB,直线PO交AB于M.请你根据圆的对称性,写出△PAB的三个正确的结论.
4、如图,PA、PB是⊙O的两条切线,A、B是切点,连接AB,直线PO交AB于M.请你根据圆的对称性,写出△PAB的三个正确的结论.
 (2012•谷城县模拟)如图,PA、PB是⊙O 的切线,切点分别是A、B,点C是⊙O上异与点A、B的点,如果∠P=60°,那么∠ACB等于
(2012•谷城县模拟)如图,PA、PB是⊙O 的切线,切点分别是A、B,点C是⊙O上异与点A、B的点,如果∠P=60°,那么∠ACB等于