题目内容
如图，PA、PB分别切⊙0于A、B，PA、BO的延长线交于点Q，连AB，若sin∠AQO=| 4 |
| 5 |
分析：利用切线的性质以及锐角三角函数关系得出sin∠AQO=
，sin∠PAE=
=
，进而利用切线长定理得出AE，BE的长，进而得出答案．
| 4 |
| 5 |
| PE |
| PA |
| 4 |
| 5 |
解答：
解：过点A作AE⊥PB于点E，
∵PA、PB分别切⊙0于A、B，
∴PA=PB，∠PBO=90°，
∴AE∥BQ，
∴∠PAE=∠Q，
∵sin∠AQO=
，
∴sin∠PAE=
=
，
设PB=4x，则PQ=5x，故PA=4x，
∴PE=
x，
∴BE=
x，
AE=
=
x，
∴tan∠ABP=
=
=3．
故选：B．
解：过点A作AE⊥PB于点E，∵PA、PB分别切⊙0于A、B，
∴PA=PB，∠PBO=90°，
∴AE∥BQ，
∴∠PAE=∠Q，
∵sin∠AQO=
| 4 |
| 5 |
∴sin∠PAE=
| PE |
| PA |
| 4 |
| 5 |
设PB=4x，则PQ=5x，故PA=4x，
∴PE=
| 16 |
| 5 |
∴BE=
| 4 |
| 5 |
AE=
| PA2-PE2 |
| 12 |
| 5 |
∴tan∠ABP=
| AE |
| EB |
| ||
|
故选：B．
点评：此题主要考查了切线的性质以及切线长定理和勾股定理以及锐角三角函数关系等知识，根据已知表示出AE，BE的长是解题关键．
练习册系列答案
53随堂测系列答案
相关题目
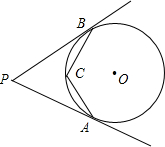如图，PA、PB分别切圆O于A、B两点，C为劣弧AB上一点，已知∠P=50°，则∠ACB=
7、如图，PA、PB分别切圆O于A、B两点，C为劣弧AB上一点，∠APB=30°，则∠ACB=（ ）
7、如图，PA，PB分别切⊙O于点A，B，点C是AB上一点，过C作⊙O的切线，交PA，PB于点D，E，若PA=6cm，则△PDE的周长是
（2012•绵阳）如图，PA、PB分别切⊙O于A、B，连接PO、AB相交于D，C是⊙O上一点，∠C=60°．
如图，PA，PB分别切⊙O于点A和点B，C是