题目内容
(2012•槐荫区二模)(1)某路段改造工程中,需沿AC方向开山修路(如图1所示),为了加快施工进度,要在小山的另一边同时施工.从AC上的一点B取∠ABD=140°,BD=1000米,∠D=50°.为了使开挖点E在直线AC上,那么DE的距离应该是多少米?(供选用的三角函数值:sin50°≈0.7660,cos50°≈0.6428,tan50°≈1.192)
(2)如图,PA、PB是⊙O的切线,AC是⊙O的直径,∠P=50°,求∠BOC的度数.
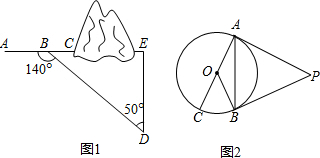
(2)如图,PA、PB是⊙O的切线,AC是⊙O的直径,∠P=50°,求∠BOC的度数.

分析:(1)先判断出△BED的形状,再根据锐角三角函数的定义进行解答即可.
(2)利用切线的性质可以得到:∠OAP=∠OBP=90°,根据四边形的内角和定理即可求得∠AOB的度数,即可求得∠BOC的度数.
(2)利用切线的性质可以得到:∠OAP=∠OBP=90°,根据四边形的内角和定理即可求得∠AOB的度数,即可求得∠BOC的度数.
解答:解:(1)∵∠ABD=140°,∠D=50°,
∴∠E=∠ABD-∠D=140°-50°=90°,
∴
=cos∠D,
∴
=0.6428,
解得DE=642.8米.
答:DE的距离应该是642.8米.
(2)∵PA、PB是⊙O的切线,
∴∠OAP=∠OBP=90°,
∵∠P=50°,
∴∠AOB=360°-90°-90°-50°=130°,
又∵AC是⊙O的直径,
∴∠BOC=180°-130°=50°.
∴∠E=∠ABD-∠D=140°-50°=90°,
∴
| DE |
| BD |
∴
| DE |
| 1000 |
解得DE=642.8米.
答:DE的距离应该是642.8米.
(2)∵PA、PB是⊙O的切线,
∴∠OAP=∠OBP=90°,
∵∠P=50°,
∴∠AOB=360°-90°-90°-50°=130°,
又∵AC是⊙O的直径,
∴∠BOC=180°-130°=50°.
点评:(1)本题考查的是解直角三角形在实际生活中的运用,涉及到三角形内角和定理及锐角三角函数的定义,熟知以上知识是解答此题的关键.
(2)本题考查了切线的性质,以及四边形的内角和定理,正确理解切线的性质是关键.
(2)本题考查了切线的性质,以及四边形的内角和定理,正确理解切线的性质是关键.

练习册系列答案
相关题目
 (2012•槐荫区二模)如图,点B的坐标是(4,4),作BA⊥x轴于点A,作BC⊥y轴于点C,反比例函数
(2012•槐荫区二模)如图,点B的坐标是(4,4),作BA⊥x轴于点A,作BC⊥y轴于点C,反比例函数