题目内容
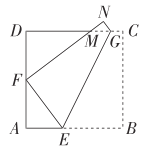
【题目】如图,在正方形ABCD中,DC=8,现将四边形BEGC沿折痕EG(G,E分别在DC,AB边上)折叠,其顶点B,C分别落在边AD上和边DC的上部,其对应点设为F,N点,且FN交DC于M.
特例体验:
(1)当FD=AF时,△FDM的周长是多少?
类比探究:
(2)当FD≠AF≠0时,△FDM的周长会发生变化吗?请证明你的猜想.
拓展延伸:
(3)同样在FD≠AF≠0的条件下,设AF为x,被折起部分(即:四边形FEGN)的面积为S,试用含x的代数式表示S,并问:当x为何值时,S=26?
【答案】(1)16;(2)不变,证明见解析;(3)![]() 当x=2或6时,四边形FEGN的面积为26.
当x=2或6时,四边形FEGN的面积为26.
【解析】
(1)如图1中,在△AEF中,设AE=x,则EF=8-x,AF=4,∠A=90°,理由勾股定理构建方程求出x,再根据△AEF∽△DFM,可得![]() ,由此即可解决问题;
,由此即可解决问题;
(2)△FDM的周长与(1)中结论相同.证明方法与(1)类似;
(3)作GK⊥AB于K.连接BF交GE于P.由△AFB≌△KEG,可得FB=GE,由(2)可知:AE=![]() ,设AF=EK=x,AK=AE+EK=AF+AE=
,设AF=EK=x,AK=AE+EK=AF+AE=![]() ,根据S=
,根据S=![]() ,构建二次函数即可解决问题;
,构建二次函数即可解决问题;
解:(1)在△AEF中,设AE=x,则EF=8-x,AF=4,∠A=90°,
由勾股定理,得:42﹢x2=(8-x)2,
∴x=3,
∴AE=3,EF=5.
∴△AEF的周长为12,
如图,
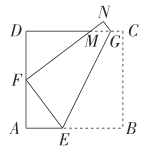
∵∠MFE=90°,
∴∠DFM+∠AFE=90°
又∵∠A=∠D=90,∠AFE=∠DMF,
∴△AEF∽△DFM,
∴![]() =
=![]() =
=![]() ,
,
∴△FDM的周长为16;
(2)△FDM的周长不会发生变化;
理由:如下图,
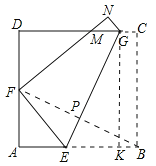
设AF=x,EF=8-AE,x2+AE2=(8-AE)2,
∴AE=![]() ,
,
∵△AEF∽△DFM,
∴![]() ,
,
∴△FMD的周长: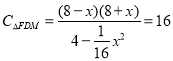 .
.
(3)如图,作GK⊥AB于K.连接BF交GE于P.

∵B、F关于GE对称,
∴BF⊥EG,
∴∠FBE=∠KGE,
在正方形ABCD中,GK=BC=AB,∠A=∠EKG=90°,
∴△AFB≌△KEG,
∴FB=GE,
由(2)可知:AE=![]() ,
,
∴AF=EK=x,AK=AE+EK=AF+AE=![]() ,
,
∴梯形AEGD的面积为:![]() ,
,
∴![]() ,
,
当S=26时,有
![]() ,
,
解得:x=2或x=6,
∴当x=2或6时,四边形FEGN的面积为26.

 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案