��Ŀ����
����Ŀ����ͼ����������x�ύ��A��B���㣬��y�ύ�ڵ�C��0����2������A�������ǣ�2��0����PΪ�������ϵ�һ�����㣬����P��PD��x���ڵ�D����ֱ��BC�ڵ�E�������ߵĶԳ�����ֱ��x����1��
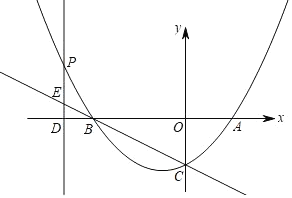
��1���������ߵĺ�������ʽ��
��2������P�ڵڶ������ڣ���PE��![]() OD�����PBE�������
OD�����PBE�������
��3���ڣ�2���������£���MΪֱ��BC��һ�㣬��x����Ϸ����Ƿ���ڵ�M��ʹ��BDM����BDΪ���ĵ��������Σ������ڣ������M�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��y��![]() x2+
x2+![]() x��2����2��
x��2����2��![]() ����3��M������
����3��M������![]() ��
��![]() ����
����![]() ��
��![]() ����
����
��������
��1����A��2��0������B��-4��0���������ı���ʽΪ��y=a��x-2����x+4��=a��x2+2x-8����������⣻
��2��PE=![]() OD����PE=��
OD����PE=��![]() x2+
x2+![]() x-2-
x-2-![]() x+2��=
x+2��=![]() ��-x��������D��-5��0��������S��PBE=
��-x��������D��-5��0��������S��PBE=![]() PE��BD=
PE��BD=![]() ��
��![]() x2+
x2+![]() x-2-
x-2-![]() x+2����-4-x����������⣻
x+2����-4-x����������⣻
��3�������������⼴�ɣ��ٵ�BD��BMʱ���ڵ�BD��DM��M����ʱ��
��1����A�������ǣ�2��0���������ߵĶԳ�����ֱ��x����1�����B����4��0����
�����ı���ʽΪ��y��a��x��2����x+4����a��x2+2x��8����
�ѵ�C��0��-2������ã���8a����2����ã�a��![]() ��
��
�������ߵı���ʽΪ��y��![]() x2+
x2+![]() x��2��
x��2��
��2������B��C���������һ�κ�������ʽ��y��mx+n����ã�
ֱ��BC�ı���ʽΪ��y����![]() x��2����tan��ABC��
x��2����tan��ABC��![]() ����sin��ABC��
����sin��ABC��![]() ��
��
���D��x��0�������P��x��![]() x2+
x2+![]() x��2������E��x����
x��2������E��x����![]() x��2����
x��2����
��PE��![]() OD��OD����x��
OD��OD����x��
��PE����![]() x2+
x2+![]() x��2+
x��2+![]() x+2����
x+2����![]() x2+x��
x2+x��
��![]() x2+x=-
x2+x=-![]() x��
x��
��ã�x��0��5����ȥx��0����
����D����5��0����
S��PBE��![]() ��PE��BD��
��PE��BD��![]() ��
��![]() x2+
x2+![]() x��2+
x��2+![]() x+2������4��x����
x+2������4��x����![]() ��
��
��3��������ã���BDM����BDΪ���ĵ��������Σ�
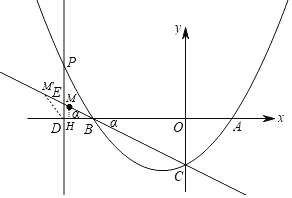
����BD��BMʱ������M��MH��x���ڵ�H��
BD��1��BM��
��MH��yM��BMsin��ABC��1��![]() ��
��![]() ��
��
��xM��![]() ��
��
�ʵ�M��![]() ��
��![]() ����
����
����BD��DM��M����ʱ��
ͬ���ɵã���M������![]() ��
��![]() ����
����
�ʵ�M����Ϊ����![]() ����
����![]() ����
����![]() ��
��![]() ����
����

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�����Ŀ���뽭��ij��ѧ�Ĺ��커������Ӽס���������ѡ��һ�����߱Ƚ�����Ķ�Ա���λ����֣�ÿ����ÿ����Ա�����ߣ���λ��cm������:
�� | 178 | 177 | 179 | 179 | 178 | 178 | 177 | 178 | 177 | 179 |
�Ҷӣ�

�������ݣ������������ݵ�ƽ��������λ�����������������±���ʾ��
��������������:
ƽ���� | ��λ�� | ���� | ���� | |
�� | 178 | 178 | b | 0.6 |
�Ҷ� | 178 | a | 178 | c |
��1������a=______��b=______��c=______��
��2�����ݱ����е����ݣ�����Ϊѡ���ĸ��ӱȽϺã���˵�����ɣ�