题目内容
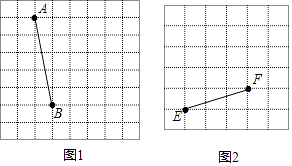
【题目】已知AB为⊙O的直径,BM为⊙O的切线,点C为射线BM上一点,连接AC交⊙O于点D,点E为BC上一点.连接AE交半圆于F.
(1)如图1,若AE平分∠BAC,求证:∠DBF=∠CBF;
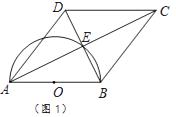
(2)如图2,过点D作⊙O的切线交BM于N,若DN⊥BM,求证:△ABC为等腰直角三角形;
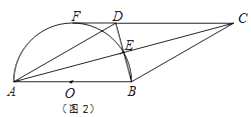
(3)在(2)的条件下,如图3,延长BF交AC于G,点H为AB上一点,且BH=2BE,过点H作AE的垂线交AC于P,连接OG交DN于K,若AP=CG,EF=1,求GK的长.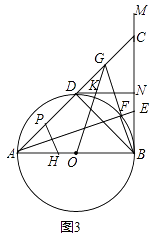
【答案】
(1)解:证明:如图1中,
∵AB是直径,BM是切线,
∴∠AFB=∠ABC=90°,
∵∠FAB+∠ABF=90°,∠ABF+∠CBF=90°,
∴∠CBF=∠FAB,
∵AE平分∠BAC,
∴∠EAC=∠FAB,
∵∠DBF=∠EAC,
∴∠DBF=∠CBF.
(2)解:证明:如图2中,连接DM.
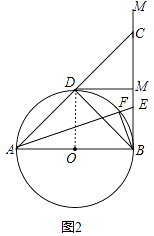
∵DM是⊙O的切线,DM⊥BC,
∴∠ODM=∠DMB=∠OBM=90°,
∴四边形ODMB是矩形,
∵OD=OB,
∴四边形ODMB是正方形,
∴∠DBO=45°,
∵AB是直径,
∴∠ADB=90°,
∴∠DAB=45°,∵∠ABC=90°,
∴∠BAC=∠ACB=45°,
∴△ABC是等腰直角三角形.
(3)解:如图3中,连接PB,作CM⊥BC交HP的延长线于M,延长BG交CM于N,作GR⊥AB于R,交DN于T.
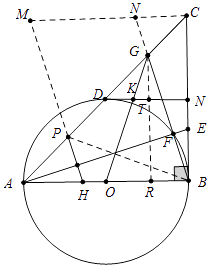
∵AP=CG,∠BAP=∠BCG=45°,BA=BC,
∴△BAP≌△BCG,
∴BP=BG,
∴∠BPG=∠BGP,
∵HM⊥AE,BN⊥AE,
∴HM∥BN,∵MN∥BH,
∴四边形MNBH是平行四边形,
∴MN=BH,
∵∠APH=∠CPM=∠BGP=∠BPG,
PC=PC,∠PCB=∠PCM,
∴△PCM≌△PCB,
∴CM=BC=AB,
∵BC=AB,∠ABE=∠BCN,易证∠BAE=∠CBN,
∴△ABE≌△BCN,
∴BE=CN,设BE=CN=a,则BH=MN=2a,
∴CM=BC=AB=3a,
∴AH=BE=a,
∵△BFE∽△ABE,
∴ ![]() =
= ![]() =
= ![]() ,
,
∵EF=1,
∴BF=3,BE= ![]() =
= ![]() ,
,
∴AH=CN=BE= ![]() ,AB=BC=CM=3
,AB=BC=CM=3 ![]() ,
,
∵AH∥CM,
∴ ![]() =
= ![]() =
= ![]() ,
,
∵AP=CG,
∴AP=DP=DG=CG,
∵GR∥BC,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴AR=GR= ![]() ,OR=RB=
,OR=RB= ![]() ,
,
在Rt△GOR中,GO= ![]() =
= ![]() ,
,
∵DK∥OA,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴GK= ![]() .
.
【解析】(1)由AB是直径和MB是⊙O的切线,易证得∠CBF=∠FAB,再根据角平分线的定义和同弧所对的圆周角相等,可证得结论。
(2)根据题意,易证得四边形ODMB是正方形,根据正方形的每一条对角线平分一组对角,得到∠DBO=45°,再由圆周角的性质,可证得∠BAC=∠ACB=45°,即可得出△ABC是等腰直角三角形.
(3)先证明△BAP≌△BCG得出BP=BG,再证明四边形MNBH是平行四边形,得出MN=BH,然后证明△PCM≌△PCB、△ABE≌△BCN得出对应边相等,设BE=CN=a,则BH=MN=2a,易证△PCM≌△PCB,建立方程求出相关线段的长,根据勾股定理及平行得线段成比例,建立方程,求解即可求得GK的值。
【考点精析】关于本题考查的平行四边形的判定与性质和切线的判定定理,需要了解若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积;切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线才能得出正确答案.

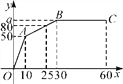
【题目】为了了解某市九年级学生学业考试体育成绩,现从中随机抽取部分学生的体育成绩进行分段(A:50分; B:49-45分;C:44-40分;D:39-30分;E:29-0分).每段包含最高分,不包含最低分,统计表如下,统计图如图所示.
分数段 | 频数(人) | 百分比 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

根据上面提供的信息,回答下列问题:
(1)在统计表中,![]() 的值为___,
的值为___, ![]() 的值为__,并将统计图补充完整.
的值为__,并将统计图补充完整.
(2)成绩在40分以上定为优秀,那么该市今年10440名九年级学生中体育成绩为优秀的学生约有多少名?