题目内容
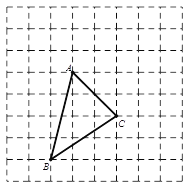
【题目】如图,在由边长为1的小正方形组成的网格图中有一个格点三角形ABC.(注:顶点均在网格线交点处的三角形称为格点三角形)
(1)请直接写出sin∠ABC的值: ;
(2)请在图中画格点三角形DEF,使得△DEF∽△ABC,且相似比为2∶1;
(3)请在图中确定格点M,使得△BCM的面积为6.如果符合题意的格点M不止一个,请分别用M1、M2、M3…表示.
【答案】(1)![]() ;(2)作图见解析;(2)作图见解析.
;(2)作图见解析;(2)作图见解析.
【解析】试题分析:(1)过点C作CD⊥AB于点D,有勾股定理求出CD,在Rt△BCD中,求sin∠DBC的值即可;
(2)依据△DEF∽△ABC,且相似比为2∶1,即可得到格点三角形DEF;
(3)构造面积为12的平行四边形即可.
试题解析:(1)过点C作CD⊥AB于点D,如图:

由勾股定理知:AB=![]() =
=![]() ,BC=
,BC=![]() =
=![]() ;AC=
;AC=![]() =
=![]() ,
,
设BD=x,则AD=![]() -x,
-x,
由题意得:BC2-BD2=AC2-AD2,
即(![]() )2-x2=(
)2-x2=(![]() )2-(
)2-(![]() -x)2,
-x)2,
解得:x=![]() ,CD=
,CD=![]() ,
,
∴sin∠ACB= =
=![]() ;
;
(2)如图:

(3)符合条件的点M有三个,如图:

练习册系列答案
相关题目
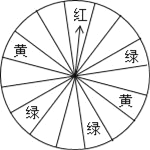
【题目】“六一”儿童节期间,某商厦为了吸引顾客,设立了一个可以自由转动的转盘(转盘被平均分成16份),并规定:顾客每购买100元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准哪个区域,顾客就可以获得相应的奖品.
颜色 | 奖品 |
红色 | 玩具熊 |
黄色 | 童话书 |
绿色 | 彩笔 |
小明和妈妈购买了125元的商品,请你分析计算:
(1)小明获得奖品的概率是多少?
(2)小明获得童话书的概率是多少?