��Ŀ����
����Ŀ����ƽ��ֱ������ϵ�У����κ���![]() ��ͼ����
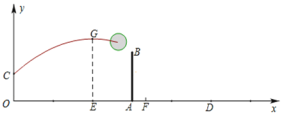
��ͼ����![]() �ύ��A����3��0����B��1��0�����㣬��y�ύ�ڵ�C��
�ύ��A����3��0����B��1��0�����㣬��y�ύ�ڵ�C��

��1����������κ����Ľ���ʽ��
��2����P��ֱ��AC�Ϸ�����������һ���㣬�Ƿ���ڵ�P��ʹ��ACP�������������ڣ������P�����ꣻ�������ڣ�˵�����ɣ�
��3����Q��ֱ��AC�Ϸ�����������һ���㣬����Q��QE��ֱ��![]() �ᣬ����ΪE���Ƿ���ڵ�Q��ʹ�Ե�B��Q��EΪ���������������AOC���ƣ������ڣ�ֱ��д����Q�����ꣻ�������ڣ�˵�����ɣ�
�ᣬ����ΪE���Ƿ���ڵ�Q��ʹ�Ե�B��Q��EΪ���������������AOC���ƣ������ڣ�ֱ��д����Q�����ꣻ�������ڣ�˵�����ɣ�
���𰸡���1��![]()
��2�����ڵ�![]() ��ʹ��ACP��������
��ʹ��ACP��������
��3��������Q��������![]() ��
��![]()
��������
���������26���⣺��1����������![]() ����A����3��0����B��1��0����
����A����3��0����B��1��0����
��![]() ����������������������������������������������1��
����������������������������������������������1��
��� ��������������������������������������������������2��
��������������������������������������������������2��
����κ����Ĺ�ϵ����ʽ![]() ����������������������3��
����������������������3��
��2������PO����PM��x����M��PN��y����N����4��
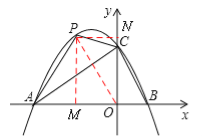
���P������m��n������![]() ��
��
PM =![]() ��
��![]() ��AO=3����5�֣�
��AO=3����5�֣�
��![]() ʱ��
ʱ��![]() ������
������
��OC=2������������������������������������������������6��
![]() ��
��![]()
��![]() ��
��![]() ��8��
��8��
��![]() ��������0���൱
��������0���൱![]() ʱ������
ʱ������![]()
![]() �����ֵ��
�����ֵ��
��ʱ![]()
![]() ��
��![]() �� ��������9��
�� ��������9��
����ڵ�![]() ��ʹ��ACP���������� ����������������������10��
��ʹ��ACP���������� ����������������������10��
��3��������Q��������![]() ��
��![]() ��������������������������12��
��������������������������12��
�֡�BQE�ס�AOC����EBQ�ס�AOC����QEB�ס�AOC����������ۿ��ó���