题目内容
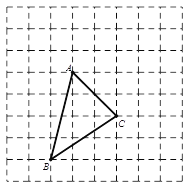
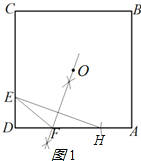
【题目】(1)如图1,△ABC中,∠C=90°,AB的垂直平分线交AC于点D,连接BD. 若AC=2,BC=1,则△BCD的周长为___________________.
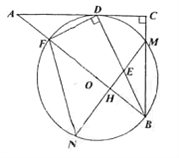
(2)O为正方形ABCD的中心,E为CD边上一点,F为AD边上一点,且△EDF的周长等于AD的长.
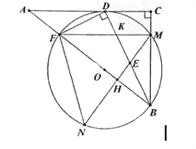
①在图2中求作△EDF.(要求:尺规作图,不写作法,保留作图痕迹)
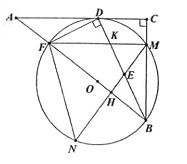
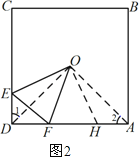
②在图3中补全图形,求∠EOF的度数.
③若![]() ,则
,则![]() =_______________.
=_______________.

图1 图2 图3
【答案】(1)3;(2)①作图见解析;②45°;③![]() .
.
【解析】试题分析:(1)由线段垂直平分线的性质得出BD=AD,得出△BCD的周长=BC+CD+BD=BC+AC,即可得出结果;
(2)①在AD上截取AH=DE,再作EG的垂直平分线,交AD于F,△EDF即为所求;
②连接OA、OD、OH,由正方形的性质得出∠1=∠2=45°,由SAS证明△ODE≌△OAH,得出∠DOE=∠AOH,OE=OH,得出∠EOH=90°,证出EF=HF,由SSS证明△EOF≌△HOF,得出∠EOF=∠HOF=45°即可;
③作OG⊥CD于G,OK⊥AD于K,设AF=8t,则CE=9t,设OG=m,由正方形的性质得出GE=CE-CG=9t-m,DE=2CG-CE=2m-9t,FK=AF-KA=8t-m,DF=2DK-AF=2m-8t,由HL证明Rt△EOG≌Rt△HOK,得出GE=KH,因此EF=GE+FK=17t-2m,由勾股定理得出方程,解方程求出m=6t,得出OG=OK=6t,GE=9t-m=9t-6t=3t,FK=8t-m=2t,由勾股定理即可得出结果.
试题解析:(1)∵AB的垂直平分线交AC于点D,
∴BD=AD,
∴△BCD的周长=BC+CD+BD=BC+AC=1+2=3,
故答案为:3;
(2)①如图1所示:△EDF即为所求;
②如图2所示:
AH=DE,连接OA、OD、OH,
∵点O为正方形ABCD的中心,
∴OA=OD,∠AOD=90°,∠1=∠2=45°,
在△ODE和△OAH中,
 ,
,
∴△ODE≌△OAH(SAS),
∴∠DOE=∠AOH,OE=OH,
∴∠EOH=90°,
∵△EDF的周长等于AD的长,
∴EF=HF,
在△EOF和△HOF中,
 ,
,
∴△EOF≌△HOF(SSS),
∴∠EOF=∠HOF=45°;
③作OG⊥CD于G,OK⊥AD于K,如图3所示:

设AF=8t,则CE=9t,设OG=m,
∵O为正方形ABCD的中心,
∴四边形OGDK为正方形,CG=DG=DK=KA=![]() AB=OG,
AB=OG,
∴GE=CE﹣CG=9t﹣m,DE=2CG﹣CE=2m﹣9t,FK=AF﹣KA=8t﹣m,DF=2DK﹣AF=2m﹣8t,
由(2)②知△EOF≌△HOF,
∴OE=OH,EF=FH,
在Rt△EOG和Rt△HOK中,
![]() ,
,
∴Rt△EOG≌Rt△HOK(HL),
∴GE=KH,
∴EF=GE+FK=9t﹣m+8t﹣m=17t﹣2m,
由勾股定理得:DE2+DF2=EF2,
∴(2m﹣9t)2+(2m﹣8t)2=(17t﹣2m)2,
整理得:(m+6t)(m﹣6t)=0,
∴m=6t,
∴OG=OK=6t,GE=9t﹣m=9t﹣6t=3t,FK=8t﹣m=2t,
∴ =
=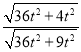 =
=![]() =
=![]() .
.
故答案为![]() .
.

【题目】为声援扬州“运河申遗”,某校举办了一次运河知识竞赛,满分10分,学生得分为整数,成绩达到6分以上(包括6分)为合格,达到9分以上(包含9分)为优秀.这次竞赛中甲乙两组学生成绩分布的条形统计图如图所示.

(1)补充完成下面的成绩统计分析表:
组别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
甲组 | 6.7 | 3.41 | 90% | 20% | |
乙组 | 7.5 | 1.69 | 80% | 10% |
(2)小明同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上表可知,小明是 组的学生;(填“甲”或“乙”)
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你给出两条支持乙组同学观点的理由.