题目内容
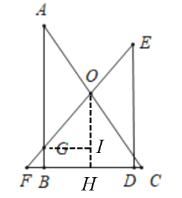
【题目】如图,为一幅重叠放置的三角板,其中∠ABC=∠EDF=90°,BC与DF共线,将△DEF沿CB方向平移,当EF经过AC的中点O时,直线EF交AB于点G,若BC=3,则此时OG的长度为( )

A.![]() B.
B.![]()
C.![]() D.
D.![]()
【答案】A
【解析】
分别过O作OH⊥BC,过G作GI⊥OH,由O是中点,根据平行线等分线段定理,可得H为BC的中点,则可得BH=![]() ,再由三个角都是直角的四边形是矩形,可得GI=BH=
,再由三个角都是直角的四边形是矩形,可得GI=BH=![]() ,在等腰直角三角形OGI中,即可求解.
,在等腰直角三角形OGI中,即可求解.
解:过O作OH⊥BC于H,过G作GI⊥OH于I
∵∠ABC=90°,
∴AB⊥BC,
∴OH∥AB,
又O为中点,
∴H为BC的中点,
∴BH=![]() BC=
BC=![]()
∵GI⊥OH,
∴四边形BHIG为矩形,
∴GI∥BH,GI=BH=![]() ,
,
又∠F=45°,
∴∠OGI=45°,
∴在Rt△OGI中,![]() .
.
故选:A

练习册系列答案
相关题目