题目内容
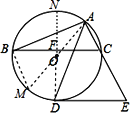
【题目】如图,△ABC内接于⊙O,AD平分∠BAC交⊙O于点D,过点D作DE∥BC交AC的延长线于点E.

(1)试判断DE与⊙O的位置关系,并证明你的结论;
(2)若∠E=60°,⊙O的半径为5,求AB的长.
【答案】(1)DE与⊙O相切,理由见解析;(2)![]() .
.
【解析】试题分析:(1)连接DO并延长到圆上一点N,交BC于点F.由AD平分∠BAC可得![]() ,由垂径定理可得DO⊥BC,再由DE∥BC,即可推导得出;
,由垂径定理可得DO⊥BC,再由DE∥BC,即可推导得出;
(2)连接AO并延长到圆上一点M,连接BM.由DE∥BC,可推导得出∠M=60°,现利用勾股定理即可得出AB的长.
试题解析:(1)DE与⊙O相切,理由如下:
连接DO并延长到圆上一点N,交BC于点F.
∵AD平分∠BAC交⊙O于点D,∴∠BAD=∠DAC,
∴![]() ,∴DO⊥BC.
,∴DO⊥BC.
∵DE∥BC,∴∠EDO=90°,∴DE与⊙O相切;
(2)连接AO并延长到圆上一点M,连接BM.
∵DE∥BC,∴∠ACB=∠E=60°,∴∠M=60°.
∵⊙O的半径为5,∴AM=10,∴BM=5,则![]() .
.

练习册系列答案
相关题目