题目内容
【题目】如图1,在矩形ABCD中,E是CB延长线上一个动点,F、G分别为AE、BC的中点,FG与ED相交于点H.
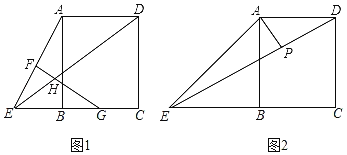
(1)求证:HE=HG;
(2)如图2,当BE=AB时,过点A作AP⊥DE于点P,连接BP,求![]() 的值;
的值;
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)连接AG,并延长AG交DC的延长线于M,连接EM,证明先证明△ABG≌△MCG(ASA),得到GA=GM,加上已知F为AE的中点,进而证明FG是△AEM的中位线,根据中位线的性质可得∠HGE=∠MEC,接下来用SAS证明△DEC≌△MEC,可得∠DEC=∠MEC,所以∠HEG=∠HGE,HE=HG即得以证明;
(2)过点B作BQ⊥BP交DE于Q,在△ABP和△EBQ中,根据三角形内角和定理及对顶角相等的性质,易得∠BEQ=∠BAP,由∠QBP=∠ABE=90°可得∠QBP=∠ABE=90°,又因为BE=AB,所以满足ASA,△BEQ≌△BAP可证;再根据全等三角形的性质可得BQ=BP,PA=QE,可证△PBQ是等腰直角三角形,![]() ,而PQ=
,而PQ=![]() PB,等量代换代入所求比例式,即可求解.
PB,等量代换代入所求比例式,即可求解.
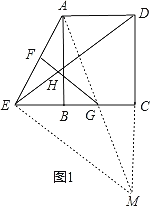
(1)证明:连接AG,并延长AG交DC的延长线于M,连接EM,
 ,
,
∵G为BC的中点,
∴BG=CG,
∵四边形ABCD是矩形,
∴∠ABG=∠DCB=90°,
∴∠ABG=∠MCG=90°,
在△ABG和△MCG中,
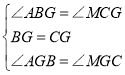 ,
,
∴△ABG≌△MCG(ASA),
∴GA=GM,
∵F为AE的中点,
∴FA=FE,
∴FG是△AEM的中位线,
∴FG∥EM,
∴∠HGE=∠MEC,
在△DCE和△MCE中,
![]()
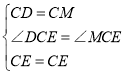 ,
,
∴△DEC≌△MEC(SAS),
∴∠DEC=∠MEC,
∵∠HGE=∠MEC,
∴∠HEG=∠HGE,
∴HE=HG;
(2)过点B作BQ⊥BP交DE于Q,则∠QBP=90°,
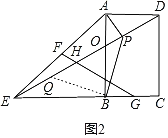
∵AP⊥DE,四边形ABCD是矩形,
∴∠APE=∠ABE=90°,
∵∠APO+∠AOP+∠BAP=180°,∠EOB+∠ABE+∠BEP=180°,∠AOP=∠EOB,
∴∠BEQ=∠BAP,
∵∠QBP=∠ABE=90°,
∴∠EBQ=∠ABP=90°﹣∠ABQ,
在△ABP和△EBQ中,
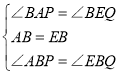 ,
,
∴△BEQ≌△BAP(ASA),
∴BQ=BP,PA=QE,
∴△PBQ是等腰直角三角形,
∴PQ=![]() PB,
PB,
∴![]() .
.

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案【题目】有30箱苹果,以每箱20千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
与标准质质量的差 (单位:千克) |
|
|
| 1 | 2 |
箱数 | 2 | 6 | 10 | 8 | 4 |
(1)这30箱苹果中,最重的一箱比最轻的一箱重多少千克?
(2)与标准质量比较,这30箱苹果总计超过或不足多少千克?
(3)若苹果每千克售价6元,则出售这30箱苹果可卖多少元?