Question

【题目】如图在△ABC 中，AB、AC 边的垂直平分线相交于点 O，分别交 BC 边于点 M、N，连接 AM，AN．

（1）若△AMN 的周长为 6，求 BC 的长；

（2）若∠MON=30°，求∠MAN 的度数；

（3）若∠MON=45°，BM=3，BC=12，求 MN 的长度．

Answer 1

【答案】（1）6；（2）120°（3）5．

【解析】

（1）根据垂直平分线的性质可得BM=AM，CN=AN，再根据三角形的周长即可求出BC；

（2）设射线OM交AB于E，射线ON交AC于F，根据四边形的内角和，即可求出∠EAF，再根据三角形的内角和，即可求出∠B＋∠C，然后根据等边对等角即可求出∠MAB＋∠NAC，从而求出∠MAN；

（3）设射线OM交AB于E，射线ON交AC于F，根据四边形的内角和，即可求出∠EAF，再根据三角形的内角和，即可求出∠B＋∠C，然后根据等边对等角即可求出∠MAB＋∠NAC，从而求出∠MAN，设MN=x，根据勾股定理列出方程求出x即可．

解：（1）∵AB、AC 边的垂直平分线相交于点 O，分别交 BC 边于点 M、N，

∴BM=AM，CN=AN

∵△AMN 的周长为 6，

∴AM＋AN＋MN=6

∴BC=BM＋MN＋CN= AM＋MN＋AN =6；

（2）设射线OM交AB于E，射线ON交AC于F，

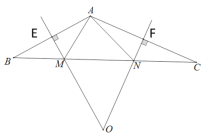
在四边形AEOF中，∠EAF=360°－∠AEO－∠AFO－∠MON=150°

∴∠B＋∠C=180°－∠BAC=30°

∵BM=AM，CN=AN

∴∠MAB=∠B，∠NAC=∠C

∴∠MAB＋∠NAC=30°

∴∠MAN=∠EAF－（∠MAB＋∠NAC）=120°；

（3）设射线OM交AB于E，射线ON交AC于F，

在四边形AEOF中，∠EAF=360°－∠AEO－∠AFO－∠MON=135°

∴∠B＋∠C=180°－∠BAC=45°

∵BM=AM=3，CN=AN

∴∠MAB=∠B，∠NAC=∠C

∴∠MAB＋∠NAC=45°

∴∠MAN=∠EAF－（∠MAB＋∠NAC）=90°

设MN=x，则AN =CN=BC－BM－MN=9－x

在Rt△AMN中，MN2=AM2＋AN2

即x2=32＋（9－x）2

解得：x=5

即MN=5