题目内容
【题目】如图,在 13×7 的网格中,每个小正方形边长都是 1,其顶点叫做格点,如图 A、B、D、E 均为格点,![]() ABD 为格点三角形.
ABD 为格点三角形.

(1)请在给定的网格中画 ABCD,要求 C 点在格点上;
(2)在(1)中 ABCD 右侧,以格点 E 为其中的一个顶点,画格点![]() EFG,并使 EF=5,FG=3,EG=
EFG,并使 EF=5,FG=3,EG=![]()
(3)先将(2)中的线段 EF 向右平移 6 个单位、再向下平移 l 个单位到 MP 的位置,再以 MP 为对角线画矩形 MNPQ(M、N、P、Q 按逆时针方向排列),直接写出矩形 MNPQ 的面积为 ______
【答案】(1)见解析;(2)见解析;(3)作图见解析,矩形MNPQ的面积为12
【解析】
(1)依据A、B、D的位置,即可得到平行四边形ABCD;
(2)依据EF=5,FG=3,EG=![]() ,即可得到
,即可得到![]() EFG的位置;
EFG的位置;
(3)依据平移的方向和距离,即可得到MP的位置,再以MP为对角线画矩形MNPQ即可得,进而得到矩形的面积.
解:(1)如图所示,四边形ABCD即为所求;
(2)如图所示,![]() EFG即为所求;
EFG即为所求;
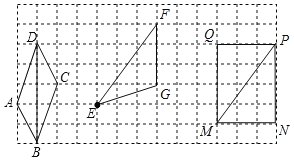
(3)如图所示,矩形MNPQ即为所求;矩形MNPQ的面积为3×4=12;
故答案为:12.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目