Question

【题目】已知二次函数y＝ax2＋bx－2的图象与x轴交于A，B两点，与y轴交于点C，点A的坐标为(4，0)，且当x＝－2和x＝5时二次函数的函数值y相等．

(1)求实数a，b的值；

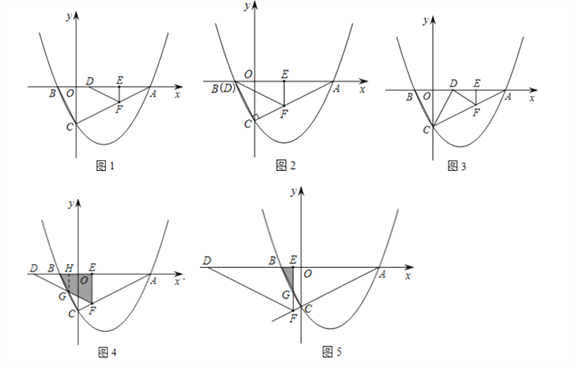
(2)如图①，动点E，F同时从A点出发，其中点E以每秒2个单位长度的速度沿AB边向终点B运动，点F以每秒个单位长度的速度沿射线AC方向运动．当点E停止运动时，点F随之停止运动．设运动时间为t秒．连接EF，将△AEF沿EF翻折，使点A落在点D处，得到△DEF.

①是否存在某一时刻t，使得△DCF为直角三角形？若存在，求出t的值；若不存在，请说明理由；

②设△DEF与△ABC重叠部分的面积为S，求S关于t的函数关系式．

Answer 1

【答案】（1）， ；（2）①t＝或t＝ ，②.

【解析】试题分析：（1）根据抛物线图象经过点A以及“当x=﹣2和x=5时二次函数的函数值y相等”两个条件，列出方程组求出待定系数的值．

（2）①首先由抛物线解析式能得到点A、B、C三点的坐标，则线段OA、OB、OC的长可求，进一步能得出AB、BC、AC的长；首先用t 表示出线段AD、AE、AF（即DF）的长，则根据AE、EF、OA、OC的长以及公共角∠OAC能判定△AEF、△AOC相似，那么△AEF也是一个直角三角形，及∠AEF是直角；若△DCF是直角，可分成三种情况讨论：

i）点C为直角顶点，由于△ABC恰好是直角三角形，且以点C为直角顶点，所以此时点B、D重合，由此得到AD的长，进而求出t的值；

ii）点D为直角顶点，此时∠CDB与∠CBD恰好是等角的余角，由此可证得OB=OD，再得到AD的长后可求出t的值；

iii）点F为直角顶点，当点F在线段AC上时，∠DFC是锐角，而点F在射线AC的延长线上时，∠DFC又是钝角，所以这种情况不符合题意．

②此题需要分三种情况讨论：

i）当点E在点A与线段AB中点之间时，两个三角形的重叠部分是整个△DEF；

ii）当点E在线段AB中点与点O之间时，重叠部分是个不规则四边形，那么其面积可由大直角三角形与小钝角三角形的面积差求得；

iii）当点E在线段OB上时，重叠部分是个小直角三角形．

试题解析：解：（1）由题意得： ，解得：a=，b=．

（2）①由（1）知二次函数为.∵A（4，0），∴B（﹣1，0），C（0，﹣2），∴OA=4，OB=1，OC=2，∴AB=5，AC=，BC=，∴AC2+BC2=25=AB2，∴△ABC为直角三角形，且∠ACB=90°．

∵AE=2t，AF=t，∴.

又∵∠EAF=∠CAB，∴△AEF∽△ACB，∴∠AEF=∠ACB=90°，∴△AEF沿EF翻折后，点A落在x轴上点D处；

由翻折知，DE=AE，∴AD=2AE=4t，EF=AE=t．

假设△DCF为直角三角形，当点F在线段AC上时：

ⅰ）若C为直角顶点，则点D与点B重合，如图2，∴AE=AB=t=÷2=；

ⅱ）若D为直角顶点，如图3．∵∠CDF=90°，∴∠ODC+∠EDF=90°．

∵∠EDF=∠EAF，∴∠OBC+∠EAF=90°，∴∠ODC=∠OBC，∴BC=DC．

∵OC⊥BD，∴OD=OB=1，∴AD=3，∴AE=，∴t=；

当点F在AC延长线上时，∠DFC＞90°，△DCF为钝角三角形．

综上所述，存在时刻t，使得△DCF为直角三角形，t=或t=．

②ⅰ）当0＜t≤时，重叠部分为△DEF，如图1、图2，∴S=×2t×t=t2；

ⅱ）当＜t≤2时，设DF与BC相交于点G，则重叠部分为四边形BEFG，如图4，过点G作GH⊥BE于H，设GH=m，则BH= ，DH=2m，∴DB=．

∵DB=AD﹣AB=4t﹣5，∴ =4t﹣5，∴m=（4t﹣5），

∴S=S△DEF﹣S△DBG=×2t×t﹣（4t﹣5）×（4t﹣5）=；

ⅲ）当2＜t≤时，重叠部分为△BEG，如图5．

∵BE=DE﹣DB=2t﹣（4t﹣5）=5﹣2t，GE=2BE=2（5﹣2t），∴S=×（5﹣2t）×2（5﹣2t）=4t2﹣20t+25．

综上所述： ．