题目内容
【题目】如图,己知正方形ABCD的边长为4, P是对角线BD上一点,PE⊥BC于点E, PF⊥CD于点F,连接AP, EF,给出下列结论:①PD=![]() EC;②四边形PECF的周长为8;③△APD一定是等腰三角形;④AP=EF;⑤EF的最小值为
EC;②四边形PECF的周长为8;③△APD一定是等腰三角形;④AP=EF;⑤EF的最小值为![]() ;⑥AP⊥EF,其中正确结论的序号为( )
;⑥AP⊥EF,其中正确结论的序号为( )

A.①②④⑤⑥B.①②④⑤C.②④⑤D.②④
【答案】A
【解析】
①根据正方形的对角线平分对角的性质,得△PDF是等腰直角三角形,在Rt△DPF中,DP2=DF2+PF2=EC2+EC2=2EC2,求得DP=![]() EC.
EC.
②先证明四边形PECF为矩形,根据等腰直角三角形和矩形的性质可得其周长为2BC,则四边形PECF的周长为8;
③根据P的任意性可以判断△APD不一定是等腰三角形;
④由②可知,四边形PECF为矩形,则通过正方形的轴对称性,证明AP=EF;
⑤当AP最小时,EF最小,EF的最小值等于2![]() ;
;
⑥证明∠PFH+∠HPF=90°,则AP⊥EF.
①如图,延长FP交AB与G,连PC,延长AP交EF与H,
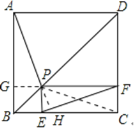
∵GF∥BC,
∴∠DPF=∠DBC,
∵四边形ABCD是正方形
∴∠DBC=45°
∴∠DPF=∠DBC=45°,
∴∠PDF=∠DPF=45°,
∴PF=EC=DF,
∴在Rt△DPF中,DP2=DF2+PF2=EC2+EC2=2EC2,
∴DP=![]() EC.故①正确;
EC.故①正确;
②∵PE⊥BC,PF⊥CD,∠BCD=90°,
∴四边形PECF为矩形,
∴四边形PECF的周长=2CE+2PE=2CE+2BE=2BC=8,故②正确;
③∵点P是正方形ABCD的对角线BD上任意一点,∠ADP=45度,
∴当∠PAD=45度或67.5度或90度时,△APD是等腰三角形,
除此之外,△APD不是等腰三角形,
故③错误.
④∵四边形PECF为矩形,
∴PC=EF,
由正方形为轴对称图形,
∴AP=PC,
∴AP=EF,
故④正确;
⑤由EF=PC=AP,
∴当AP最小时,EF最小,
则当AP⊥BD时,即AP=![]() BD=
BD=![]() ×4
×4![]() =2
=2![]() 时,EF的最小值等于2
时,EF的最小值等于2![]() ,故⑤正确;
,故⑤正确;
⑥∵GF∥BC,
∴∠AGP=90°,
∴∠BAP+∠APG=90°,
∵∠APG=∠HPF,
∴∠PFH+∠HPF=90°,
∴AP⊥EF,
故⑥正确;
本题正确的有:①②④⑤⑥;
故选:A.