题目内容
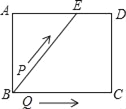
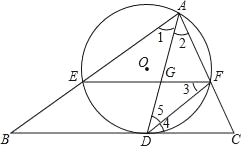
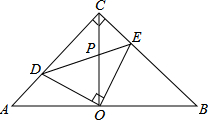
【题目】如图,在等腰直角△ABC中,∠ACB=90°,O是斜边AB的中点,点D,E分别在直角边AC,BC上,且∠DOE=90°,DE交OC于点P.则下列结论:(1)AD+BE=AC;(2)AD2+BE2=DE2;(3)△ABC的面积等于四边形CDOE面积的2倍;(4)OD=OE.其中正确的结论有( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
由等腰直角三角形的性质可得AC=BC,CO=AO=BO,∠ACO=∠BCO=∠A=∠B=45°,CO⊥AO,由“ASA”可证△ADO≌△CEO,△CDO≌△BEO,由全等三角形的性质可依次判断.
∵在等腰直角△ABC中,∠ACB=90°,O是斜边AB的中点,
∴AC=BC,CO=AO=BO,∠ACO=∠BCO=∠A=∠B=45°,CO⊥AO
∵∠DOE=90°,
∴∠COD+∠COE=90°,且∠AOD+∠COD=90°
∴∠COE=∠AOD,且AO=CO,∠A=∠ACO=45°,
∴△ADO≌△CEO(ASA)
∴AD=CE,OD=OE,故④正确,
同理可得:△CDO≌△BEO
∴CD=BE,
∴AC=AD+CD=AD+BE,故①正确,
在Rt△CDE中,CD2+CE2=DE2,
∴AD2+BE2=DE2,故②正确,
∵△ADO≌△CEO,△CDO≌△BEO
∴S△ADO=S△CEO,S△CDO=S△BEO,
∴△ABC的面积等于四边形CDOE面积的2倍;故③正确,
综上所述:正确的结论有①②③④,
故选D.

【题目】八(1)班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表:
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的方差;
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是 队.
【题目】一个运输公司有甲、乙两种货车,两次满载的运输情况如下表:
甲种货车辆数 | 乙种货车辆数 | 合计运货吨数 | |
第一次 | 2 | 4 | 18 |
第二次 | 5 | 6 | 35 |
(1)求甲、乙两种货车每次满载分别能运输多少吨货物;
(2)现有一批重34吨的货物需要运输,而甲、乙两种货车运输的保养费用分别为80元/辆和40元/辆.公司打算由甲、乙两种货车共10辆来完成这次运输,为了使保养费用不超过700元,公司该如何安排甲、乙两种货车来完成这次运输任务.