Question

【题目】综合与探究如图，直线的解析式为，且与轴交于点，直线经过点和点，直线，交于点，连接．

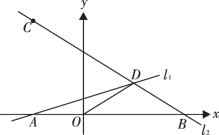
（1）求直线的解析式；

（2）求证：是等腰三角形；

（3）求的面积；

（4）探究在直线上是否存在异于点的另一点，使得与的面积相等，若存在，请直接写出点的坐标；若不存在，说明理由．

Answer 1

【答案】（1）；（2）详见解析；（3）9；（4）点的坐标是．

【解析】

（1）设直线的解析式为，将点和点代入求解即可；

（2）联立l1和l2的解析式，得出点的坐标为，过点作轴于点，则，证明即可；

（3）根据题意可得出点的坐标为，从而可得，即可得出；

（4）根据与的面积相等和，，可得点P的纵坐标为2或-2，再根据点的坐标为，可得出点P的纵坐标为-2，即可求出点P的坐标．

解：（1）设直线的解析式为，

∵直线经过点，和点，

∴，

解得，

∴直线的解析式为；

（2）证明：联立方程组，

得，

∴点的坐标为，

过点作轴于点，则，

∵点的坐标为，

∴，

∴，

在和中，

∴，

∴，

∴是等腰三角形；

（3）由，令，解方程，得，

∴点的坐标为，

∴，

∴；

（4）∵与的面积相等，由（3）可得，，

∴点P的纵坐标为2或-2，

∵点的坐标为，

∴点P的纵坐标为-2，

将点P的纵坐标代入直线的解析式为，

可得-2=，

解答x=9，

∴点的坐标是．