题目内容
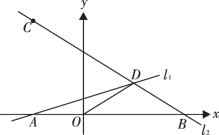
【题目】如图,在所给的正方形网格中,每个小正方形的边长均为1个单位,每个小正方形的顶点称为格点.格点△ABD中,A(-3,5)、B(-7,2)、D(0,2) .

(1) 作出□ABCD,并直接写出C点坐标为_______;
(2) 作出BD的中点M
(3) 在y轴上作出点N(不与点D重合),使得∠NAD=∠NBD.
【答案】(1)图见解析,![]() ;(2)图见解析;(3)图见解析.
;(2)图见解析;(3)图见解析.
【解析】
(1)分别过点B作AD的平行线、过点D作AB的平行线,两条平行线的交点即为点C;先根据平行四边形的性质可得点A平移到点D的平移方式与点B平移到点C的平移方式相同,再根据点A、D的坐标得出平移方式,由此即可得出点C的坐标;
(2)根据平行四边形的性质,连接AC,与BD的交点即为中点M;
(3)过点A作AB的垂线,与y轴的交点即为点N,理由:设BN的中点为点P,连接PA、PD,根据直角三角形的性质可得![]() ,再利用圆周角定理即可得证.
,再利用圆周角定理即可得证.
(1)分别过点B作AD的平行线、过点D作AB的平行线,两条平行线的交点即为点C,作图结果如下所示:

由平行四边形的性质可知,点A平移到点D的平移方式与点B平移到点C的平移方式相同
![]()
![]() 点A平移到点D的平移方式为:先向右平移3个单位长度,再向下平移3个单位长度
点A平移到点D的平移方式为:先向右平移3个单位长度,再向下平移3个单位长度
![]()
![]() 点C的坐标为
点C的坐标为![]() ,即
,即![]()
故答案为:![]() ;
;
(2)平行四边形的性质:对角线互相平分
连接AC,与BD的交点即为中点M,如图所示:

(3)如图,过点A作AB的垂线,与y轴的交点即为点N,理由如下:
设BN的中点为点P,连接PA、PD
![]() 点P为BN的中点
点P为BN的中点
![]() PA为
PA为![]() 斜边上的中线,PD为
斜边上的中线,PD为![]() 斜边上的中线
斜边上的中线
![]() ,
,![]()
![]()
则以点P为圆心,PA的长为半径画圆,一定经过点![]()
由圆周角定理得:![]() .
.


练习册系列答案
相关题目