题目内容
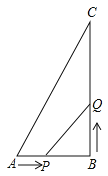
【题目】如图,在平面直角坐标系中,已知点A(0,2),△AOB为等边三角形,P是x轴上一个动点(不与原点O重合),以线段AP为一边在其右侧作等边三角形APQ.
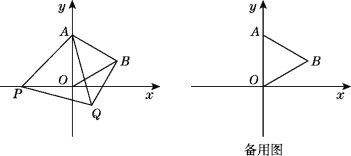
(1)求点B的坐标.
(2)在点P运动过程中,∠ABQ的大小是否发生改变?若不改变,求出其大小;若改变,请说明理由.
(3)连接OQ,当OQ∥AB时,求点P的坐标.
【答案】(1) 点B的坐标为(![]() ,1);(2)∠ABQ的大小始终不变,∠ABQ=90°;(3) P的坐标为(-
,1);(2)∠ABQ的大小始终不变,∠ABQ=90°;(3) P的坐标为(-![]() ,0)
,0)
【解析】
(1)过点B作BC⊥x轴于点C,根据等边三角形的性质可得∠AOB=60°,BO=OA=2,从而求出∠BOC=30°,然后根据30°所对的直角边是斜边的一半和勾股定理即可求出BC和OC,从而求出点B的坐标;
(2)根据等边三角形的性质可得AP=AQ,AO=AB,∠PAQ=∠OAB=60°,从而证出∠PAO=∠QAB,然后利用SAS证出△APO≌△AQB,从而得出∠ABQ=∠AOP=90°;
(3)根据题意,画出图形,然后根据平行线的性质可得∠BQO=90°,∠BOQ=∠ABO=60°,从而求出∠OBQ=30°,然后根据30°所对的直角边是斜边的一半和勾股定理即可求出OQ和BQ,再根据(2)中全等可得OP=BQ,从而求出点P的坐标.
解:(1)如图①,过点B作BC⊥x轴于点C.
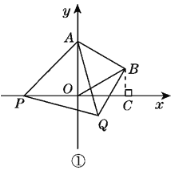
∵△AOB为等边三角形,且OA=2,
∴∠AOB=60°,BO=OA=2.
∴∠BOC=30°.
又∵∠OCB=90°,
∴BC=![]() OB=1,OC=
OB=1,OC=![]() .
.
∴点B的坐标为(![]() ,1).
,1).
(2)∠ABQ的大小始终不变.
∵△APQ,△AOB均为等边三角形,
∴AP=AQ,AO=AB,∠PAQ=∠OAB=60°.
∴∠PAO=∠QAB.
在△APO与△AQB中,

∴△APO≌△AQB(SAS).
∴∠ABQ=∠AOP=90°.
(3)如图②,当OQ∥AB时,点P在x轴的负半轴上,点Q在点B的下方,
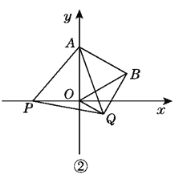
∵AB∥OQ,
∴∠BQO=180°-∠ABQ=90°,∠BOQ=∠ABO=60°.
∴∠OBQ=30°.
又OB=OA=2,
∴OQ=![]() OB=1,BQ=
OB=1,BQ=![]() ,
,
由(2)可知,△APO≌△AQB,
∴OP=BQ=![]() .
.
∴此时点P的坐标为(-![]() ,0).
,0).

 怎样学好牛津英语系列答案
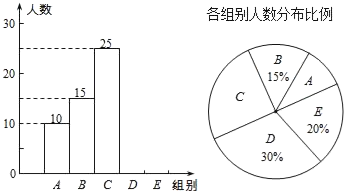
怎样学好牛津英语系列答案【题目】某校举行全体学生“汉字听写”比赛,每位学生听写汉字39个.随机抽取了部分学生的听写结果,绘制成如下的图表.
组别 | 正确字数x | 人数 |
A | 0≤x<8 | 10 |
B | 8≤x<16 | 15 |
C | 16≤x<24 | 25 |
D | 24≤x<32 | m |
E | 32≤x<40 | n |
根据以上信息完成下列问题:
(1)统计表中的m= ,n= ,并补全条形统计图;
(2)扇形统计图中“C组”所对应的圆心角的度数是 ;
(3)已知该校共有900名学生,如果听写正确的字的个数少于24个定为不合格,请你估计该校本次听写比赛不合格的学生人数.