题目内容
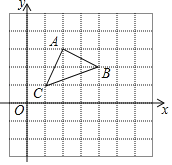
【题目】在如图所示平面直角坐标系中,每个小正方形的边长均为1,△ABC的三个顶点均在格点上.
(1)以O为旋转中心,将△ABC逆时针旋转90°,画出旋转后的△A1B1C1;
(2)画出△A1B1C1关于原点对称的△A2B2C2;
(3)若△ABC内有一点P(a,b),结果上面两次变换后点P在△A2B2C2中的对应点为P′,则点P′的坐标为 .

【答案】(1)作图见解析;(2)作图见解析;(3)点P′的坐标为(b,﹣a).
【解析】试题分析:(1)令起始边垂直,终边垂直.(2)把每个顶点坐标取相反数,连接.
(3) P′和P先逆时针旋转90°(横坐标变纵坐标的相反数,纵坐标等于横坐标),再作原点对称(横纵坐标都取相反数).
试题解析:
(1)如图,△A1B1C1为所作;
(2)如图,△A2B2C2为所作;

(3)P(a,b)第一次变换后P1(- b,a),第二次变换后点坐标为P′(b,﹣a).

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目