题目内容
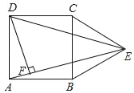
【题目】正方形ABCD中,E,F分别是AB与BC边上的中点,连接AF,DE,BD,交于G,H(如图所示)。求AG:GH:HF的值。
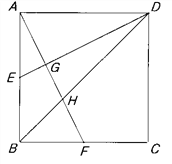
【答案】AG:GH:HF=6:4:5
【解析】试题分析:如图,延长DE,CD交于点M,易证AD=DM,通过△AED∽△BME得![]() ,
,
即AD=MB,同理, △AGD∽△FMG, 则![]() ,
, ,所以AG=
,所以AG= ![]() ,设AG=2a,则FG=3a,AF=5a,同理△AHD∽△FBH,则
,设AG=2a,则FG=3a,AF=5a,同理△AHD∽△FBH,则![]() ,即
,即![]() ,∴AH=2FH,所以
,∴AH=2FH,所以![]() 所以
所以![]() ,所以
,所以![]() .
.
试题解析:

如图,延长DE,CB交于点M,
∵四边形ABCD是正方形,
∴AD∥BC,AD=BC=AB,
∵点E是AB的中点,点F是BC的中点,则FM=![]() AD,
AD,
∴AE=BE, BF= ![]() ,
,
易证△AED∽△BME,
∴![]() ,
,
∴![]() ,即AD=MB,
,即AD=MB,
同理,△AGD∽△FMG,
则![]() ,
, ,所以AG=
,所以AG= ![]() ,
,
设AG=2a,则FG=3a,AF=5a,
同理△AHD∽△FBH,则![]() ,即
,即![]() ,
,
∴AH=2FH,
所以![]()
所以![]() ,
,
所以![]() .
.
点睛:本题考查了相似三角形的判定与性质以及正方形的性质,在判定两个三角形相似时,应注意利用图形中已有的公共角,公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形.

练习册系列答案
相关题目