题目内容
(25分)如图,在Rt△ABC中,∠B=90°,它的内切圆分别与边BC、CA、AB相切于点D、E、F,联结AD与内切圆相交于另一点P,联结PC、PE、PF.已知PC⊥PF.求证:
(1)EP/DE=PD/DC;(2)△EPD是等腰三角形.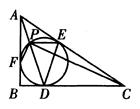
(1)EP/DE=PD/DC;(2)△EPD是等腰三角形.

(1)如图,联结DF.则△BDF是等腰直角三角形.于是,∠FPD=∠FDB=45°.故∠DPC=45°.
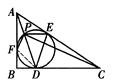
又因为∠PDC=∠PFD,所以,△PFD∽△PDC.
从而,PF/FD=PD/DC.①
由∠AFP=∠ADF,∠AEP=∠ADE,
得△AFP∽△ADF,△AEP∽△ADE.
于是,EP/DE=AP/AE=AP/AF=FP/DF.
故由式①得EP/DE=PD/DC.
(2)因为∠EPD=∠EDC,结合式②得△EPD’∽△EDC.所以,△EPD也是等腰三角形.

又因为∠PDC=∠PFD,所以,△PFD∽△PDC.
从而,PF/FD=PD/DC.①
由∠AFP=∠ADF,∠AEP=∠ADE,
得△AFP∽△ADF,△AEP∽△ADE.
于是,EP/DE=AP/AE=AP/AF=FP/DF.
故由式①得EP/DE=PD/DC.
(2)因为∠EPD=∠EDC,结合式②得△EPD’∽△EDC.所以,△EPD也是等腰三角形.
略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
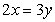 ,则
,则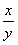 等于
等于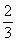
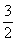
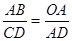
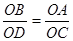
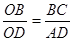
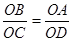
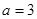 cm,
cm,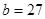 cm,则线段
cm,则线段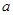 ,
,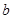 的比例中项为 cm.
的比例中项为 cm. 与
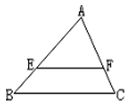
与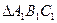 是关于点O为位似中心的位似图形,他们的顶点都在格点上.
是关于点O为位似中心的位似图形,他们的顶点都在格点上.
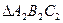 使它与的位似比等于3
使它与的位似比等于3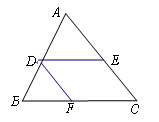
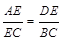
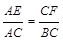
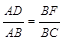
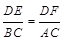
 ( )
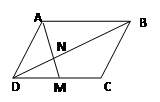
( )
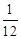
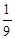
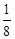
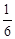
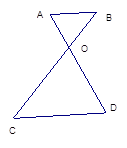
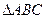 中,
中,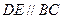 ,
,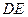 分别交边
分别交边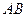 、
、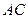 与
与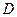 、
、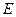 两点,若
两点,若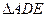 与
与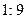 ,则
,则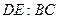 的比值为 .
的比值为 .