题目内容
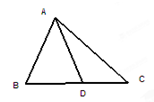
如图,在平行四边形ABCD中,点M为CD的中点,AM与
BD相交于点N,那么 ( )
( )
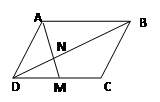
BD相交于点N,那么
 ( )
( )
A.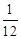 | B.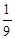 | C.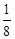 | D.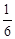 |
A
由平行四边形可证三角形的相似性,然后根据相似比求出面积比.
解:∵AB∥CD
∴△ABN∽△MDN
∴AN:MN=AB:MD=2:1
∴S△DMN:S△ADN=1:2,即S△DMN=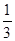 S△ADM又S△ADM=
S△ADM又S△ADM= S?ABCD
S?ABCD
故S△DMN:S?ABCD=1:12.
故选A
注意根据已知条件求得有关线段的比,再根据面积公式进行求面积的比
解:∵AB∥CD
∴△ABN∽△MDN
∴AN:MN=AB:MD=2:1
∴S△DMN:S△ADN=1:2,即S△DMN=
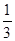 S△ADM又S△ADM=
S△ADM又S△ADM= S?ABCD
S?ABCD故S△DMN:S?ABCD=1:12.
故选A
注意根据已知条件求得有关线段的比,再根据面积公式进行求面积的比

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
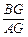 的值.
的值.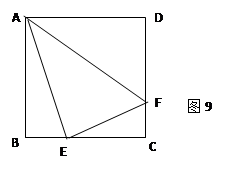
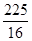 B、
B、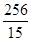 C、
C、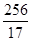 D、
D、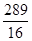

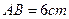 ,
,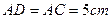 .点
.点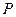 由
由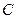 出发沿
出发沿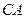 方向匀速运动,速度为
方向匀速运动,速度为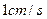 ;同时,线段
;同时,线段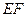 由
由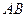 出发沿
出发沿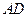 方向匀速运动,速度为
方向匀速运动,速度为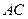 于
于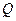 ,连接
,连接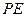 、
、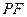 .若设运动时间为
.若设运动时间为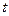 (s)(
(s)(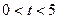 ).解答下列问题:
).解答下列问题: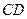 ?并求出此时
?并求出此时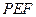 的形状,并请说明理由.
的形状,并请说明理由.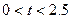 时,
时,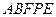 的面积 ▲ (填序号)
的面积 ▲ (填序号)
 ④不变
④不变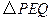 的面积为
的面积为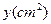 ,求出
,求出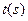 之间的函数关系式及
之间的函数关系式及 的取值范围.
的取值范围.