��Ŀ����
����Ŀ���Ķ�����һ�����֣���ֱ������ϵ�У���֪�����������M��x1��y1����N��x2��y2������M��N����֮��ľ�������ù�ʽMN��![]() ���㣮����������⣺
���㣮����������⣺

��1������P��2��4����Q����3����8������P��Q�����ľ��룻
��2������A��1��2����B��4����2������O������ԭ�㣬�ж���AOB��ʲô�����Σ���˵�����ɣ�
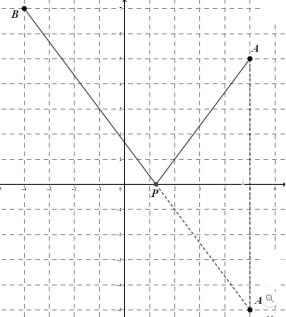
��3����֪��A(5��5)��B(-4��7)����P��x���ϣ���ҪʹPA+PB�ĺ���С����PA+PB����Сֵ��
���𰸡���1��P��Q�����ľ���PQΪ13����2����AOB��ֱ�������Σ� ���ɼ���������3��PA+PB��Сֵ=15��
��������
��1�����������ľ��빫ʽ���㣻
��2�����ݹ��ɶ������涨�����
��3������A����x��ĶԳƵ�A�����õ�A�����꣬�����ù��ɶ������м��㼴��.
(1)P��Q�����ľ���PQ��![]() ��13��
��13��
(2)��AOB��ֱ�������Σ�
�������£�AO2��(1��0)2+(2��0)2��5��
BO2��(4��0)2+(��2��0)2��20��
AB2��(4��1)2+(��2��2)2��25��
��AO2+BO2��AB2��
���AOB��ֱ��������
��3��![]()
![]() ��
��![]()
![]() ����A����x��ĶԳƵ�A������A������Ϊ��5����5����
����A����x��ĶԳƵ�A������A������Ϊ��5����5����
����A��B��x����һ�㣬�˵���ǵ�P����ʱPA+PB��С��
![]() PA+PB��Сֵ=A��B=
PA+PB��Сֵ=A��B=![]() =
=![]() =15
=15
 ��
��