题目内容
【题目】已知⊙O的半径为2,点P是⊙O内一点,且OP= ![]() ,过P作互相垂直的两条弦AC、BD,则四边形ABCD面积的最大值为( )
,过P作互相垂直的两条弦AC、BD,则四边形ABCD面积的最大值为( )
A.4
B.5
C.6
D.7
【答案】B
【解析】解:如图:连接OA、OD,作OE⊥AC于E,OF⊥BD于F,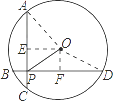
∵AC⊥BD,
∴四边形OEPF为矩形,
∵OA=OD=2,OP= ![]() ,
,
设OE为x(x>0),
根据勾股定理得,OF=EP= ![]() =
= ![]() ,
,
在Rt△AOE中,AE= ![]() =
= ![]()
∴AC=2AE=2 ![]() ,
,
同理得,BD=2DF=2 ![]() =2
=2 ![]() ,
,
又∵任意对角线互相垂直的四边形的面积等于对角线乘积的 ![]() ,
,
∴S四边形ABCD= ![]() AC×BD=
AC×BD= ![]() ×2
×2 ![]() ×2
×2 ![]() =2
=2 ![]() =2
=2 ![]()
当x2= ![]() 即:x=
即:x= ![]() 时,四边形ABCD的面积最大,等于2
时,四边形ABCD的面积最大,等于2 ![]() =5.
=5.
答案为:B.
作出弦心距,根据S四边形ABCD=对角线乘积的一半,列出函数关系式,配成顶点式,求出最值.

练习册系列答案
相关题目