题目内容
【题目】如图，直线y＝﹣2x+4与x轴、y轴分别交于A、B两点，P是直线AB上的一个动点，点C的坐标为（﹣4，0），PC交y轴点于D，O是原点．
（1）求△AOB的面积；
（2）线段AB上存在一点P，使△DOC≌△AOB，求此时点P的坐标；
（3）直线AB上存在一点P，使以P、C、O为顶点的三角形面积与△AOB面积相等，求出P点的坐标．
【答案】（1）△AOB的面积是4；（2）点P的坐标是（
，
）；（3）点P的坐标为：（1，2）或（3，﹣2）．
【解析】
（1）利用直线解析式易求得点A、B的坐标，从而得到线段OA=2，OB=4．所以根据直角三角形的面积公式来求△AOB的面积；
（2）根据全等三角形的对应边相等求得线段OD=OA=2，则易求点D的坐标．由点C、D的坐标易求得直线CD的方程，则点P是直线CD与直线AB的交点；
（3）设P（x，y）．根据点C的坐标易求得线段OC=4．所以由直角三角形的面积公式列出关于y的方程，通过解方程可以求得点P的坐标．
解：（1）如图1，∵直线y＝﹣2x+4与x轴、y轴分别相交于A、B两点，
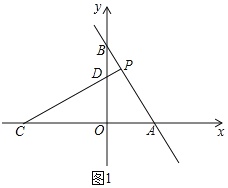
∴A（2，0），B（0，4），
∴OA＝2，OB＝4．
∴SAOB＝
OAOB＝×2×4＝4，即△AOB的面积是4；
（2）∵△DOC≌△AOB，
∴OD＝OA＝2，
∴D（0，2）．
故设直线CD的解析式为y＝kx+2（k≠0）．
∵C（﹣4，0）
则0＝﹣4k+2，
解得，k＝，
∴直线CD的解析式为y＝x+2．
又∵点P是直线CD与直线AB的交点，
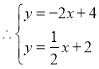
解得：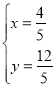 
点 
的坐标是 
（3）如图2，设P（x，y），
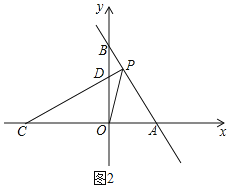
又∵点C的坐标为（﹣4，0），
∴OC＝4，
∵S△COP＝S△AOB，
∴OC×|y|＝4，即|y|＝2，
解得，y＝±2，
∵P是直线AB上一点，
∴点P的坐标为：（1，2）或（3，﹣2）．
