Question

【题目】如图，P是等边三角形ABC内一点，连接PA、PC，PA＝PC，∠APC＝90°，把线段AP绕点A逆时针旋转120°，得到线段AQ（点P与点Q为对应点），连接BQ交AP于点E．点D为BQ的中点，连接AD、PD，若S△DAP＝2，则AB＝__．

Answer 1

【答案】4

【解析】

延长QA到M，使得AM＝AQ，连接BM，PM．首先证明△PAM是等边三角形，证明△MAB≌△PAC（SAS），推出∠AMB＝∠APC＝90°，由AQ＝AM，BD＝DQ，推出AD∥BM，BM＝2AD，推出AD＝PA，再利用三角形的面积公式构建方方程求出PA即可解决问题．

延长QA到M，使得AM＝AQ，连接BM，PM．

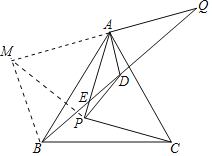
∵△ABC是等边三角形，

∴∠BAC＝60°，

∵PA＝PC，∠APC＝90°，

∴∠PAC＝∠PCA＝45°，

∵∠PAQ＝120°，

∴∠PAM＝180°﹣120°＝60°，

∵AM＝AQ＝AP，

∴△APM是等边三角形，

∴∠MAP＝∠BAC＝60°，

∴∠MAB＝∠PAC，

∵AM＝AP，AB＝AC，

∴△MAB≌△PAC（SAS），

∴BM＝PC，∠AMB＝∠APC＝90°，

∵AQ＝AM，BD＝DQ，

∴AD∥BM，BM＝2AD，

∴AD＝PA，

∴∠QAD＝∠QMB＝90°，

∴∠PAD＝∠MAD﹣∠MAP＝90°﹣60°＝30°，

∵S△PAD＝2，

∴PAADsin30°＝2，

∴PAPA＝2，

∴PA＝4，

∴AB＝AC＝PA＝4，

故答案为4．